
| A. | -$\sqrt{3}$ | B. | 0 | C. | $\sqrt{3}$ | D. | 3 |
分析 根据题意,由数列的递推公式写出数列的前几项,分析可得an+3=an,进而分析可得a2010=a3,即可得答案.
解答 解:根据题意,若a1=0,a2=$\frac{-\sqrt{3}}{1}$=-$\sqrt{3}$.
a3=$\frac{-2\sqrt{3}}{-3+1}$=$\sqrt{3}$,a4=$\frac{\sqrt{3}-\sqrt{3}}{3+1}$=0,a5=$\frac{-\sqrt{3}}{1}$=-$\sqrt{3}$,…,
由此可知,an+3=an.
又2 010=3×670,
所以a2010=a3=$\sqrt{3}$.
故选:C.
点评 本题考查数列的递推公式,关键是写出数列的前几项,分析得到规律.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:选择题
| A. | -7 | B. | 8 | C. | -8 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y′=x2cosx-2xsin x | B. | y′=2xcos x+x2sin x | ||
| C. | y′=2xcosx-x2sinx | D. | y′=xcosx-x2sin x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
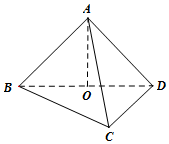 (文科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,
(文科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第三象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $-\frac{11}{3}$ | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
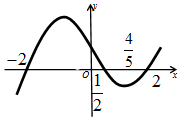
| A. | $\frac{1}{2}$为f(x)的极大值点 | B. | -2为f(x)的极大值点 | ||
| C. | 2为f(x)的极大值 | D. | $\frac{4}{5}$为f(x)的极小值点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com