
 ,中心角
,中心角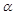 .求证:当
.求证:当 时该扇形面积最大;
时该扇形面积最大;
 .求证:
.求证: .
. (定值),而扇形面积
(定值),而扇形面积 ,一般地求二元函数最值可消元化为一元函数(见下面详解),也可考虑利用基本不等式,
,一般地求二元函数最值可消元化为一元函数(见下面详解),也可考虑利用基本不等式, 求出最值,并判断等号成立 条件,从而得解;(2)这是一个双变元(
求出最值,并判断等号成立 条件,从而得解;(2)这是一个双变元( 和
和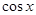 )的函数求最值问题,由于这两个变元没有制约关系,所以可先将其中一个看成主元,另一个看成参数求出最值(含有另一变元),再求解这一变元下的最值,用配方法或二次函数图象法.
)的函数求最值问题,由于这两个变元没有制约关系,所以可先将其中一个看成主元,另一个看成参数求出最值(含有另一变元),再求解这一变元下的最值,用配方法或二次函数图象法.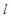 ,半径为
,半径为 ,则
,则 ,
, 2分
2分
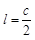 时,
时, 5分
5分 ,而
,而
 时该扇形面积最大 7分
时该扇形面积最大 7分
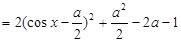 9分
9分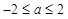 ,∴
,∴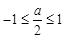 , 11分
, 11分 时,
时, 14分
14分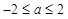 ,所以
,所以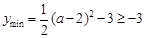 ,当
,当 时取等号,
时取等号, . 16分
. 16分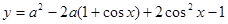
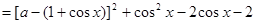 9分
9分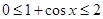 ,
,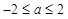 , 11分
, 11分 时,
时, , 14分
, 14分 ,∴
,∴
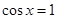 时取等号
时取等号 . 16分
. 16分

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源:不详 题型:解答题
 (弦´矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.
(弦´矢+矢2).弧田(如图),由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差. ,弦长等于9米的弧田.
,弦长等于9米的弧田.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的最大值为
的最大值为 ,最小值为
,最小值为 ,其中
,其中 .
. 、
、 的值(用
的值(用 表示);
表示); 的顶点与平面直角坐标系
的顶点与平面直角坐标系 中的原点
中的原点 重合,始边与
重合,始边与 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点 .求
.求 的值.
的值. 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 中,以x轴为始边作两个锐角
中,以x轴为始边作两个锐角 、
、 ,它们的终边分别与单位圆交于A、B两点.已知点A的横坐标为
,它们的终边分别与单位圆交于A、B两点.已知点A的横坐标为 ;B点的纵坐标为
;B点的纵坐标为 .则
.则 的值为 .
的值为 .
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 是边长为1的正三角形,曲线
是边长为1的正三角形,曲线 分别是
分别是 为圆心,
为圆心, 为半径画的弧,曲线
为半径画的弧,曲线 称为螺旋线的第一圈;然后又以A为圆心,
称为螺旋线的第一圈;然后又以A为圆心, 半径画弧,如此继续下去,这样画到第圈。设所得螺旋线
半径画弧,如此继续下去,这样画到第圈。设所得螺旋线 的总长度为
的总长度为 ,则
,则 =
= 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com