
设数列 满足:
满足: ,
, ,
, .
.
(Ⅰ)求 的通项公式及前
的通项公式及前 项和
项和 ;
;
(Ⅱ)已知 是等差数列,
是等差数列, 为前
为前 项和,且
项和,且 ,
, .求
.求 的通项公式,并证明:
的通项公式,并证明: .
.
(Ⅰ) ,
, ;(Ⅱ)
;(Ⅱ) ,证明详见解析.
,证明详见解析.
【解析】
试题分析:(Ⅰ)求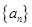 的通项公式及前
的通项公式及前 项和
项和 ,由已知
,由已知 ,
, ,
, ,数列
,数列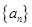 是以
是以 为首项,
为首项, 为公比等比数列,由等比数列的通项公式及前
为公比等比数列,由等比数列的通项公式及前 项和公式可得;(Ⅱ)求
项和公式可得;(Ⅱ)求 的通项公式,由
的通项公式,由 是等差数列,
是等差数列, 为前
为前 项和,且
项和,且 ,
, ,可设等差数列
,可设等差数列 的公差为
的公差为 ,根据已知条件,求出公差
,根据已知条件,求出公差 的值,从而得到
的值,从而得到 ;证明:
;证明: ,由
,由 ,分母是等差数列连续两项积,像这类数列,求其前
,分母是等差数列连续两项积,像这类数列,求其前 项和,常常采用拆项相消法,即
项和,常常采用拆项相消法,即 ,从而解出.
,从而解出.
试题解析:(Ⅰ)因为 ,又
,又 ,所以
,所以 ,因此
,因此 是首项为1,公比为3的等比数列,所以
是首项为1,公比为3的等比数列,所以 ,
, ;
;
(Ⅱ)设等差数列 的公差为
的公差为 ,依题意
,依题意 ,
, ,所以
,所以 ,即
,即 ,故
,故 . 由此得,
. 由此得, . 所以,
. 所以,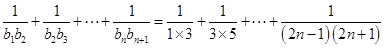

 .因此所证不等式成立.
.因此所证不等式成立.
考点:等比数列的定义及通项公式,等差数列的通项公式,拆项相消法求数列的前 项和,考查学生的运算能力以及转化与化归的能力.
项和,考查学生的运算能力以及转化与化归的能力.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
an+
|
| 1 |
| 4 |
an+
|
查看答案和解析>>
科目:高中数学 来源:2015届广西桂林十八中高二上学期段考文科数学试卷(解析版) 题型:解答题
已知等差数列 ,公差
,公差 不为零,
不为零, ,且
,且 成等比数列;
成等比数列;
⑴求数列 的通项公式;
的通项公式;
⑵设数列 满足
满足 ,求数列
,求数列 的前
的前 项和
项和 .
.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高一下学期期中考试数学试卷(解析版) 题型:解答题
已知函数 ,
, 为正整数.
为正整数.
(Ⅰ)求 和
和 的值;
的值;
(Ⅱ)数列 的通项公式为
的通项公式为 (
( ),求数列
),求数列 的前
的前 项和
项和 ;
;
(Ⅲ)设数列 满足:
满足: ,
, ,设
,设 ,若(Ⅱ)中的
,若(Ⅱ)中的 满足:对任意不小于3的正整数n,
满足:对任意不小于3的正整数n, 恒成立,试求m的最大值.
恒成立,试求m的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com