已知Sn是等比数列{an}的前n项和,an∈N+,a2=30,a1S3=999.
(Ⅰ)求an和;
(Ⅱ)设Sn各位上的数字之和为bn,求数列{bn}的前n项和Tn.
解:(Ⅰ)设等比数列{a
n}的公比为q,∵a
n∈N
*∴q>0.
又∵
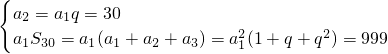
(4分)
∴
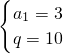
(6分)
∴a
n=3×10
n-1,
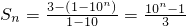
(8分)
(Ⅱ)∵S
n各位上的数字之和为b
n,
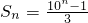
∴s
1=3?b
1=3=3×1,
s
2=33,?b
2=3+3=6=3×2,
s
3=333?b
3=3+3+3=9=3×3…
∴b
n=3n,b
n+1-b
n=3,∴{b
n}是等差数列(10分)
∴
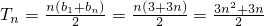
.(12分)
分析:(Ⅰ)先利用条件求出首项和公比,求出通项,再代入等比数列的求和公式即可.
(Ⅱ)有(Ⅰ)的结果求出{b
n}是等差数列,再代入等差数列的求和公式即可
点评:本题主要考查等差数列和等比数列的前n项和公式.考查学生的运算能力.
