
设函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() (
(![]() ).
).
(1)证明:![]()
![]() ;
;
(2)当![]() 时,比较
时,比较![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(3)证明:![]() (
(![]() ).
).
【考查目的】本题考查函数与导数、数学归纳法、不等式等基础知识,考查抽象概括能力、推理论证能、运算求解能力和创新意识,考查函数与方程思想、转化与化归思想
解:(1)证明:设![]() ,所以
,所以![]() …………1分
…………1分
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
即函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,在
上单调递增,在![]() 处取得唯一极小值,…2分
处取得唯一极小值,…2分
因为![]() ,所以对任意实数
,所以对任意实数![]() 均有
均有 ![]() .即
.即![]() ,
,
所以![]()
![]() ………………………………………………………………3分
………………………………………………………………3分
(2)解:当![]() 时,
时,![]()
![]() .用数学归纳法证明如下:
.用数学归纳法证明如下:
①当![]() 时,由(1)知
时,由(1)知![]()
![]() 。
。
②假设当![]() (
(![]() )时,对任意
)时,对任意![]() 均有
均有![]()
![]() ,………………5分
,………………5分
令![]() ,
,![]() ,
,
因为对任意的正实数![]() ,
,![]() ,
,
由归纳假设知,![]() .………………………………………6分
.………………………………………6分
即![]() 在
在![]() 上为增函数,亦即
上为增函数,亦即![]() ,
,
因为![]() ,所以
,所以![]() .从而对任意
.从而对任意![]() ,有
,有![]() .
.
即对任意![]() ,有
,有![]() .这就是说,当
.这就是说,当![]() 时,对任意
时,对任意![]() ,也有
,也有![]()
![]() .由①、②知,当
.由①、②知,当![]() 时,都有
时,都有![]()
![]() .……………8分
.……………8分
(2)证明1:先证对任意正整数![]() ,
,![]() .
.
由(2)知,当![]() 时,对任意正整数
时,对任意正整数![]() ,都有
,都有![]()
![]() .令
.令![]() ,得
,得![]() .所以
.所以![]() .…………………………………………………………………9分
.…………………………………………………………………9分
再证对任意正整数![]() ,
,
![]()
![]() .
.
要证明上式,只需证明对任意正整数![]() ,不等式
,不等式![]() 成立.
成立.
即要证明对任意正整数![]() ,不等式
,不等式![]() (*)成立……………………10分
(*)成立……………………10分
以下分别用数学归纳法和基本不等式法证明不等式(*):
方法1(数学归纳法):
①当![]() 时,
时,![]() 成立,所以不等式(*)成立.
成立,所以不等式(*)成立.
②假设当![]() (
(![]() )时,不等式(*)成立,即
)时,不等式(*)成立,即![]() .……………11分
.……………11分
则![]() .
.
因为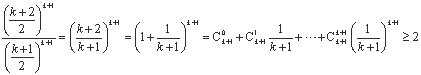
所以![]() .………………………………………13分
.………………………………………13分
这说明当![]() 时,不等式(*)也成立.由①、②知,对任意正整数
时,不等式(*)也成立.由①、②知,对任意正整数![]() ,不等式(*)都成立.
,不等式(*)都成立.
综上可知,对任意正整数![]() ,
,![]() 成立 …14分
成立 …14分



科目:高中数学 来源:2012-2013学年湖北省仙桃市高三上学期第三次考试文科数学试卷(解析版) 题型:解答题
设函数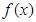 =
=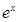 (
(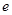 为自然对数的底数),
为自然对数的底数),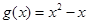 ,记
,记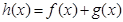 .
.
(1)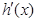 为
为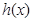 的导函数,判断函数
的导函数,判断函数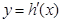 的单调性,并加以证明;
的单调性,并加以证明;
(2)若函数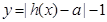 =0有两个零点,求实数
=0有两个零点,求实数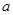 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省龙岩市高三上学期期末考试数学理卷(普通学校) 题型:解答题
.(本题满分14分)
设函数 =
=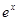 (
( 为自然对数的底数),
为自然对数的底数), ,记
,记 .
.
(Ⅰ)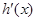 为
为 的导函数,判断函数
的导函数,判断函数 的单调性,并加以证明;
的单调性,并加以证明;
(Ⅱ)若函数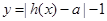 =0有两个零点,求实数
=0有两个零点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省龙岩市高三上学期期末考试数学理卷(非一级校) 题型:解答题
.(本题满分14分)
设函数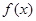 =
=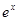 (
(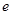 为自然对数的底数),
为自然对数的底数),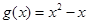 ,记
,记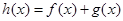 .
.
(Ⅰ)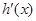 为
为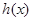 的导函数,判断函数
的导函数,判断函数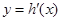 的单调性,并加以证明;
的单调性,并加以证明;
(Ⅱ)若函数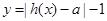 =0有两个零点,求实数
=0有两个零点,求实数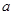 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分14分)
设函数![]() =
=![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() ,记
,记![]() .
.
(Ⅰ)![]() 为
为![]() 的导函数,判断函数
的导函数,判断函数![]() 的单调性,并加以证明;
的单调性,并加以证明;
(Ⅱ)若函数![]() =0有两个零点,求实数
=0有两个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com