
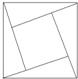
 9、如图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,现在用四种颜色给这四个直角三角形区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则有多少种不同的涂色方法( )
9、如图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,现在用四种颜色给这四个直角三角形区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则有多少种不同的涂色方法( )科目:高中数学 来源: 题型:
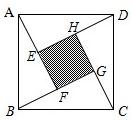 “赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).某同学随机地在大正方形及其内部区域投针,若直角三角形的两条直角边的长分别是2和1,则针扎到小正方形(阴影)区域的概率是( )
“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).某同学随机地在大正方形及其内部区域投针,若直角三角形的两条直角边的长分别是2和1,则针扎到小正方形(阴影)区域的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
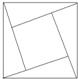 如图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,现在用四种颜色给这四个直角三角形区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则有多少种不同的涂色方法
如图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,现在用四种颜色给这四个直角三角形区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则有多少种不同的涂色方法查看答案和解析>>
科目:高中数学 来源:湖南 题型:单选题
| A.24种 | B.72种 | C.84种 | D.120种 |

查看答案和解析>>
科目:高中数学 来源:2008年湖南省高考数学试卷(单独招生)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com