
【题目】已知命题p1:函数y=2x-2-x在R上为增函数,p2:函数y=2x+2-x在R上为减函数,则在命题q1:p1∨p2,q2:p1∧p2,q3:(p1)∨p2和q4:p1∧(p2)中,真命题是
A.q1,q3
B.q2,q3
C.q1,q4
D.q2,q4
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足:对于任意的正整数
满足:对于任意的正整数![]() ,
,![]() ,
,![]() ,且
,且![]() ,则称该数列为“跳级数列”.
,则称该数列为“跳级数列”.
(1)若数列![]() 为“跳级数列”,且
为“跳级数列”,且![]() ,求
,求![]() 、
、![]() 的值;
的值;
(2)若数列![]() 为“跳级数列”,则对于任意一个大于
为“跳级数列”,则对于任意一个大于![]() 的质数
的质数![]() ,在数列
,在数列![]() 中总有一项是
中总有一项是![]() 的倍数;
的倍数;
(3)若![]() 为奇质数,则存在一个“跳级数列”
为奇质数,则存在一个“跳级数列”![]() ,使得数列
,使得数列![]() 中每一项都不是
中每一项都不是![]() 的倍数.
的倍数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车公司最近研发了一款新能源汽车,并在出厂前对100辆汽车进行了单次最大续航里程的测试。现对测试数据进行分析,得到如图所示的频率分布直方图:

(1)估计这100辆汽车的单次最大续航里程的平均值(同一组中的数据用该组区间的中点值代表).
(2)根据大量的汽车测试数据,可以认为这款汽车的单次最大续航里程![]() 近似地服从正态分布
近似地服从正态分布![]() ,经计算第(1)问中样本标准差
,经计算第(1)问中样本标准差![]() 的近似值为50。用样本平均数
的近似值为50。用样本平均数![]() 作为
作为![]() 的近似值,用样本标准差
的近似值,用样本标准差![]() 作为
作为![]() 的估计值,现任取一辆汽车,求它的单次最大续航里程恰在250千米到400千米之间的概率.
的估计值,现任取一辆汽车,求它的单次最大续航里程恰在250千米到400千米之间的概率.
参考数据:若随机变量服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
(3)某汽车销售公司为推广此款新能源汽车,现面向意向客户推出“玩游戏,送大奖”活动,客户可根据抛掷硬币的结果,操控微型遥控车在方格图上行进,若遥控车最终停在“胜利大本营”,则可获得购车优惠券3万元。已知硬币出现正、反面的概率都是0.5方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,客户每掷一次硬币,遥控车向前移动一次。若掷出正面,遥控车向前移动一格(从![]() 到
到![]() )若掷出反面遥控车向前移动两格(从
)若掷出反面遥控车向前移动两格(从![]() 到
到![]() ),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第
),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第![]() 格的概率为P试证明
格的概率为P试证明![]() 是等比数列,并求参与游戏一次的顾客获得优惠券金额的期望值。
是等比数列,并求参与游戏一次的顾客获得优惠券金额的期望值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日![]() 点的轨道运行.
点的轨道运行.![]() 点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,
点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,![]() 点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
![]() .
.
设![]() ,由于
,由于![]() 的值很小,因此在近似计算中
的值很小,因此在近似计算中![]() ,则r的近似值为
,则r的近似值为
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4,坐标系与参数方程】
在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为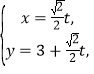 (t为参数),在以O为极点,
(t为参数),在以O为极点,![]() 轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为
轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]()
(Ⅰ)求直线![]() 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(Ⅱ)若直线![]() 与
与![]() 轴的交点为P,直线
轴的交点为P,直线![]() 与曲线C的交点为A,B,求
与曲线C的交点为A,B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某媒体为调查喜爱娱乐节目![]() 是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
是否与观众性别有关,随机抽取了30名男性和30名女性观众,抽查结果用等高条形图表示如图:
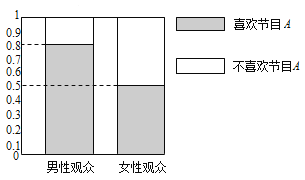
(1)根据该等高条形图,完成下列![]() 列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目
列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.05的前提下认为喜欢娱乐节目![]() 与观众性别有关?
与观众性别有关?

(2)从性观众中按喜欢节目![]() 与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目
与否,用分层抽样的方法抽取5名做进一步调查.从这5名中任选2名,求恰有1名喜欢节目![]() 和1名不喜欢节目
和1名不喜欢节目![]() 的概率.
的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
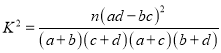 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com