
若X是离散型随机变量,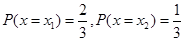 ,且
,且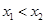 ,又已知
,又已知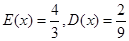 ,则
,则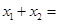 ( )
( )
A.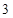 | B.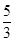 | C.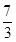 | D.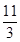 |
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:单选题
在长为12cm的线段AB上任取一点M,并以线段AM为一边作正方形,则此正方形的面积介于36cm2与81cm2之间的概率为( )
A.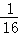 | B. | C.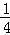 | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
某班50名学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].从样本成绩不低于80分的学生中随机选取2人,这2人中成绩在90分以上(含90分)的人数为ξ,则ξ的数学期望为( )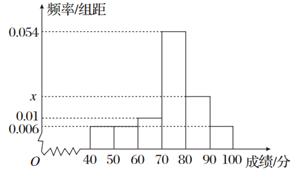
A. | B.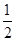 | C.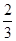 | D.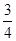 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
一数学兴趣小组利用几何概型的相关知识做试验计算圆周率,他们向一个边长为1米的正方形区域均匀撒豆,测得正方形区域有豆5120颗,正方形的内切圆区域有豆4009颗,则他们所测得的圆周率约为(保留三位有效数字)( )
| A.3.13 | B.3.14 | C.3.15 | D.3.16 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设a∈{1,2,3,4},b∈{2,4,8,12},则函数f(x)=x3+ax-b在区间[1,2]上有零点的概率为( )
A.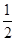 | B.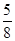 | C.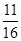 | D.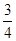 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
[2014·济南模拟]现有10张奖券,8张2元的,2张5元的,某人从中随机地、无放回地抽取3张,则此人得奖金额的数学期望是( )
| A.6 | B.7.8 | C.9 | D.12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com