分析:(Ⅰ)由题意,可以C为原点,CA,CB,CC
1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,给出各点的坐标,由于已知AM⊥BA
1.故可由向量的数量积为0证明AM⊥BC,再由线面垂直的判定定理证明AM⊥平面A
1BC;
(II)求平面ABM与平面AB
1C
1所夹锐角的余弦值,可先求出两个平面的法向量,再由公式cosθ=|
|即可求得所要的结果
解答: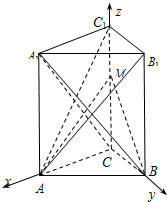
证明:(Ⅰ)如图,以C为原点,CA,CB,CC
1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则A(
,0,0),B(0,1,0),A
1(
,0,3),
B
1(0,1,3),C
1(0,0,3),
=(0,1,0),(1分)
设M(0,0,t),则
=(
,0,t),∴
•=0即AM⊥BC,又因为AM⊥BA
1,
所以 AM⊥平面A
1BC (3分)
解:(Ⅱ)
=(
,-1,3),因为AM⊥BA
1,所以
•=-3+3t=0,得t=1,
即M(0,0,1),,可得平面ABM的一个法向量为
=(1,
,
) (3分)
又
=(-
,1,3),
=(-
,0,3),,设平面AB
1C
1的一个法向量为
=(X,Y,Z),
则
•=0且
•=0,得Y=0,x=
z,,令z=1,得平面平面AB
1C
1的一个法向量为
=(
,0,1),(3分)
设平面ABM与平面AB
1C
1所夹锐角为θ,
则cosθ=|
|=
=
(2分)
点评:本题考查由向量方法证明线面垂直,求两平面的夹角,解题的关键是熟练掌握向量法解决几何问题的方法,本题的难点是正确建系,理解两向量的夹角与两平面夹角的对应关系.

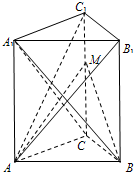 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,CB=1,CA=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,CB=1,CA= 证明:(Ⅰ)如图,以C为原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则A(
证明:(Ⅰ)如图,以C为原点,CA,CB,CC1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则A(

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案



