
(本题满分13分)已知函数 ,其中
,其中 .
.
(Ⅰ)若函数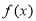 在其定义域内单调递减,求实数
在其定义域内单调递减,求实数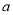 的取值范围;
的取值范围;
(Ⅱ)若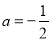 ,且关于
,且关于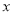 的方程
的方程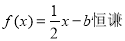 在
在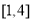 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数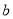 的取值范围.
的取值范围.
(Ⅰ)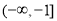 ;(Ⅱ)
;(Ⅱ)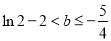 .
.
【解析】
试题分析:(Ⅰ)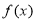 的定义域是
的定义域是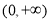 ,由于函数
,由于函数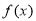 在其定义域内单调递减,所以
在其定义域内单调递减,所以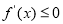 在
在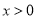 时恒成立,即
时恒成立,即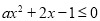 在
在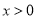 恒成立. 解法一:因为
恒成立. 解法一:因为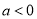 ,所以二次函数开口向下,对称轴
,所以二次函数开口向下,对称轴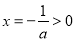 ,问题转化为
,问题转化为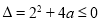 ;即可求出a的范围;解法二,分离变量,得
;即可求出a的范围;解法二,分离变量,得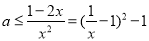 在
在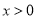 恒成立,即
恒成立,即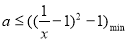
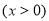 ,当
,当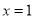 时,
时,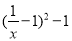 取最小值
取最小值 ,即可求出a 的范围; (Ⅱ)由题意
,即可求出a 的范围; (Ⅱ)由题意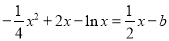 ,即
,即 ,
,
设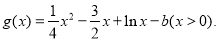 则
则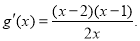 列表可知
列表可知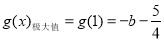 ,
, ,又
,又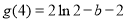 ,方程
,方程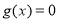 在[1,4]上恰有两个不相等的实数根.根据函数图象可知
在[1,4]上恰有两个不相等的实数根.根据函数图象可知 , 即可求出b的范围.
, 即可求出b的范围.
试题解析:【解析】
(Ⅰ)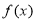 的定义域是
的定义域是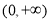 ,求导得
,求导得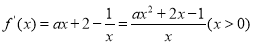
依题意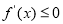 在
在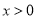 时恒成立,即
时恒成立,即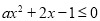 在
在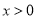 恒成立. 3分
恒成立. 3分
这个不等式提供2种解法,供参考
解法一:因为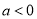 ,所以二次函数开口向下,对称轴
,所以二次函数开口向下,对称轴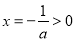 ,问题转化为
,问题转化为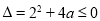
所以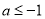 ,所以
,所以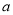 的取值范围是
的取值范围是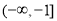 6分
6分
解法二,分离变量,得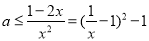 在
在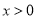 恒成立,即
恒成立,即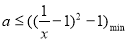
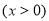
当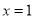 时,
时,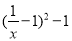 取最小值
取最小值 ,∴
,∴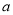 的取值范围是
的取值范围是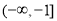 6分
6分
(Ⅱ)由题意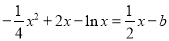 ,即
,即 ,
,
设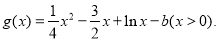 则
则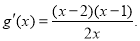 列表:
列表:
|
|
|
|
|
|
|
|
|
|
|
|
| ? | 极大值 | ? | 极小值 | ? |
∴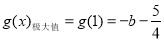 ,
, ,又
,又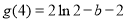 10分
10分
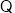 方程
方程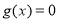 在[1,4]上恰有两个不相等的实数根.
在[1,4]上恰有两个不相等的实数根.
则 , 得
, 得 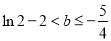 (注意
(注意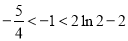 ) 13分.
) 13分.
考点:1.导数在研究函数单调性中的应用;2.函数的零点与方程的根.


科目:高中数学 来源:2015届山东师范大学附属中学高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
已知双曲线 的右焦点为F,若过点F的直线与双曲线的右支有且只有一个交点,则此直线的斜率的取值范围是( )
的右焦点为F,若过点F的直线与双曲线的右支有且只有一个交点,则此直线的斜率的取值范围是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届安徽省皖南八校高三第一次联考理科数学试卷(解析版) 题型:填空题
关于函数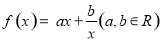 ,下列命题正确的是——(写出所有正确命题的编号)
,下列命题正确的是——(写出所有正确命题的编号)
①不论a,b取什么值,函数f(x)的图像都关于原点对称.
②若a=b≠0,则函数f(x)的极小值是2a,极大值是-2a.
③当ab≠0时,函数f(x)图像上任意一点的切线都不可能经过原点.
④当a>0,b>0时,对函数f(x)图像上任意一点A,图像上存在唯一的点B,使得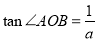 .(点O是坐标原点)
.(点O是坐标原点)
⑤当ab≠0时,函数f(x)图像上任意一点的切线与直线y=ax及y轴围成的三角形的面积是定值.
查看答案和解析>>
科目:高中数学 来源:2015届安徽省皖南八校高三第一次联考理科数学试卷(解析版) 题型:选择题
由直线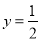 ,y=2,曲线
,y=2,曲线 及y轴所围图形的面积为( )
及y轴所围图形的面积为( )
A. 21n2 B. 21n 2-1 C.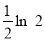 D.
D.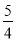
查看答案和解析>>
科目:高中数学 来源:2015届宁夏银川市高三9月月考文科数学试卷(解析版) 题型:选择题
函数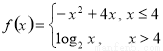 ,若函数
,若函数 在区间(
在区间(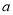 ,
,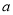 +1)上单调递增,则实数
+1)上单调递增,则实数
的取值范围是( )
A.(- ,1
,1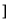 B.[1, 4]
B.[1, 4]
C. 4, +
4, + ) D.(-
) D.(- ,1
,1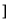 ∪[4, +
∪[4, + )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com