
分析 (1)任取4个数字,然后再排列即可.
(2)第一位数字不能为0,故有9种取法,其它3个位置任意,问题得以解决.
(3)求出个位是0,2的数的个数,个位是4,6,8的数的个数,相加即得所求.
解答 解:(1)任取4个数字,然后再排列,故有$A_{10}^4=5040$.
(2)第一位数字不能为0,故有9种取法,其它3个位置任意,故有9A93=4356,
(3)个位是0或2时,最高位是有7种取法,其它2个位置任意,共有2×7×A82=784个,
对于个位是4,6,8中的一个数字,先排个位有3种方法,
再排最高位有6种排法,其它2个位置任意,共有3×6×A82=1008个,
综上,大于3000的没有重复数字的四位偶数共有784+1008=1792
点评 本题考查排列、组合、两个基本原理的应用,排列与组合问题要区分开,题目要求元素的顺序,则是排列问题,排列问题要做到不重不漏,有些题目带有一定的约束条件,解题时要先考虑有限制条件的元素,体现了分类讨论的数学思想,属于中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | -2 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,用4种不同颜色给图中的A、B、C、D四个区域涂色,规定一个区域只涂一种颜色,相邻区域必须涂不同的颜色,则不同的涂色方案有84种(用数字作答)
如图,用4种不同颜色给图中的A、B、C、D四个区域涂色,规定一个区域只涂一种颜色,相邻区域必须涂不同的颜色,则不同的涂色方案有84种(用数字作答)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
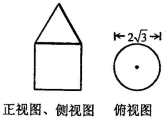 一个简单组合体的正视图和侧视图都是由一个正方形与一个正三角形构成的相同的图形,俯视图是半径为$\sqrt{3}$的圆(包括圆心),则该组合体的体积等于( )
一个简单组合体的正视图和侧视图都是由一个正方形与一个正三角形构成的相同的图形,俯视图是半径为$\sqrt{3}$的圆(包括圆心),则该组合体的体积等于( )| A. | (9+6$\sqrt{3}$)π | B. | (3+6$\sqrt{3}$)π | C. | (3+2$\sqrt{3}$)π | D. | (1+6$\sqrt{3}$)π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | an=3n-1 | B. | an=2n-1 | C. | an=3n | D. | an=2n-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | b>c>a | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | t | 70 |
| A. | 50 | B. | 55 | C. | 56.5 | D. | 55.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com