
已知 (a>0且a≠1)是定义在R上的单调递减函数,记a的所有可能取值构成集合A;P(x,y)是椭圆
(a>0且a≠1)是定义在R上的单调递减函数,记a的所有可能取值构成集合A;P(x,y)是椭圆 上一动点,
上一动点, 与点P关于直线y=x+1对称,记
与点P关于直线y=x+1对称,记 的所有可能取值构成集合B,若随机的从集合A,B中分别抽出一个元素
的所有可能取值构成集合B,若随机的从集合A,B中分别抽出一个元素 ,则
,则 的概率是___________
的概率是___________

解析试题分析:由 (a>0且a≠1)是定义在R上的单调递减函数,知A=(0,1)
(a>0且a≠1)是定义在R上的单调递减函数,知A=(0,1)
对于椭圆 ,由于原点关于y=x+1的对称点为(-1,1)
,由于原点关于y=x+1的对称点为(-1,1)
所以,椭圆关于y=x+1的对称椭圆为 ,
, 在改椭圆上,可知y1-1∈[-4,4]
在改椭圆上,可知y1-1∈[-4,4]
于是 ∈[-1,1],即B=[-1,1]
∈[-1,1],即B=[-1,1]
【方法一】由 ,分别以
,分别以 为横坐标和纵坐标,
为横坐标和纵坐标,
可知点( )构成一个面积为2的矩形
)构成一个面积为2的矩形
其中满足 的是图中阴影部分,面积为
的是图中阴影部分,面积为
所以,满足 的概率是
的概率是

【方法二】当 时,此事件发生的概率为
时,此事件发生的概率为 ,此时必有
,此时必有
当 时,此事件发生的概率为
时,此事件发生的概率为 ,此时
,此时 与
与 概率相等,各占
概率相等,各占 ,于是此时满足
,于是此时满足 的概率为
的概率为
以上两事件互斥,且[-1,0]与(0,1]的区间长度相等,故满足 的概率为
的概率为
考点:指数函数的单调性,轴对称图形,坐标的取值范围,几何概型.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:填空题
如图, 是以
是以 为圆心,半径为
为圆心,半径为 的圆的内接正方形. 将一颗豆子随机地扔到该圆内,用
的圆的内接正方形. 将一颗豆子随机地扔到该圆内,用 表示事件“豆子落在正方形
表示事件“豆子落在正方形 内”,
内”, 表示事件“豆子落在扇形
表示事件“豆子落在扇形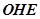 (阴影部分)内”,则
(阴影部分)内”,则 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
高一年级某班63人,要选一名学生做代表,每名学生当选是等可能的,若“选出代表是女生”的概率是“选出代表是男生”的概率的 ,这个班的女生人数为( ).
,这个班的女生人数为( ).
| A.20 | B.25 | C.35 | D.30 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
从装有 个红球和
个红球和 个黒球的口袋内任取
个黒球的口袋内任取 个球,那么互斥而不对立的两个事件是( )
个球,那么互斥而不对立的两个事件是( )
A 至少有一个黑球与都是黑球
至少有一个黑球与都是黑球  B
B
 至少有一个红球与都是黑球
至少有一个红球与都是黑球
C 至少有一个黑球与至少有
至少有一个黑球与至少有 个红球 D
个红球 D 恰有
恰有 个黑球与恰有
个黑球与恰有
 个黑球
个黑球
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
一盒中放有大小相同的10个小球,其中8个黑球、2个红球,现甲、乙二人先后各自从盒子中无放回地任意抽取2个小球,已知甲取到了2个黑球,则乙也取到2个黑球的概率是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com