
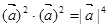 ②
②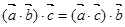 ③ |
③ |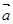 ·
·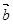 |=|
|=|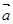 |·|
|·|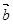 | ④若
| ④若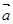 ∥
∥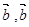 ∥
∥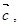 则
则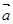 ∥
∥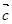 ⑤
⑤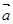 ∥
∥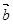 ,则存在唯一实数λ,使
,则存在唯一实数λ,使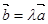 ⑥若
⑥若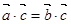 ,且
,且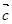 ≠
≠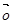 ,则
,则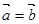 ⑦设
⑦设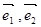 是平面内两向量,则对于平面内任何一向量
是平面内两向量,则对于平面内任何一向量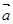 ,都存在唯一一组实数x、y,使
,都存在唯一一组实数x、y,使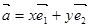 成立。 ⑧若|
成立。 ⑧若|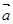 +
+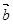 |=|
|=|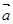 -
-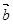 |则
|则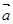 ·
·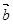 =0。 ⑨
=0。 ⑨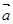 ·
·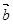 =0,则
=0,则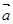 =
=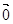 或
或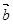 =
=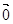
| A.1 | B.2 | C.3 | D.3个以上 |
 判断。
判断。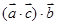 表示和向量
表示和向量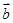 共线的向量,同理
共线的向量,同理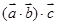 表示和向量
表示和向量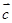 共线的向量,显然向量
共线的向量,显然向量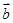 和向量
和向量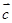 不一定是共线向量,故
不一定是共线向量,故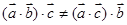 不一定成立。
不一定成立。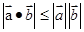
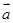 ”
”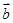 和向量
和向量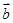 在向量
在向量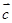 方向的投影相等即可,作图易知满足条件的向量有无数多个。
方向的投影相等即可,作图易知满足条件的向量有无数多个。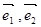 是不共线的向量即一组基底。
是不共线的向量即一组基底。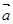 ·
·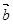 =0。
=0。

科目:高中数学 来源:不详 题型:单选题
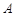 、
、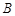 分别是射线
分别是射线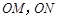 上的两点,给出下列向量:①
上的两点,给出下列向量:①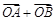 ;②
;②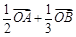 ;③
;③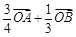 ; ④
; ④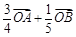 ;⑤
;⑤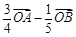 .这些向量中以
.这些向量中以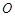 为起点,终点在阴影区域内的是( )
为起点,终点在阴影区域内的是( )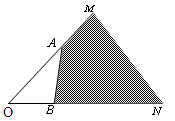
| A.①② | B.①④ | C.①③ | D.⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com