
如下图,过曲线 :
: 上一点
上一点 作曲线
作曲线 的切线
的切线 交
交 轴于点
轴于点 ,又过
,又过 作
作
 轴的垂线交曲线
轴的垂线交曲线 于点
于点 ,然后再过
,然后再过 作曲线
作曲线 的切线
的切线 交
交 轴于点
轴于点 ,又过
,又过 作
作 轴的垂线交曲线
轴的垂线交曲线 于点
于点 ,
, ,以此类推,过点
,以此类推,过点 的切线
的切线 与
与 轴相交于点
轴相交于点 ,再过点
,再过点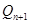 作
作 轴的垂线交曲线
轴的垂线交曲线 于点
于点 (
( N
N ).
).
(1) 求 、
、 及数列
及数列 的通项公式;(2) 设曲线
的通项公式;(2) 设曲线 与切线
与切线 及直线
及直线 所围成的图形面积为
所围成的图形面积为 ,求
,求 的表达式; (3) 在满足(2)的条件下, 若数列
的表达式; (3) 在满足(2)的条件下, 若数列 的前
的前 项和为
项和为 ,求证:
,求证:
 N
N .
.

(1) 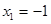 ,
,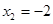 ,
,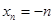 ;(2)
;(2) 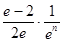 ;(3)见解析.
;(3)见解析.
【解析】
试题分析:(1)利用导数求直线切线 和切线
和切线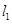 的方程,从而易得
的方程,从而易得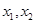 的值,再得直线
的值,再得直线 的方程,知点
的方程,知点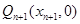 在直线
在直线 上,所以
上,所以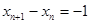 ,既得通项公式;(2)观察图形利用定积分求
,既得通项公式;(2)观察图形利用定积分求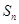 表达式;(3)分别求得
表达式;(3)分别求得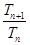 及
及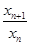 表达式,再用数学归纳法、二项式定理及导数的方法证明即可.
表达式,再用数学归纳法、二项式定理及导数的方法证明即可.
试题解析:(1) 由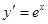 ,设直线
,设直线 的斜率为
的斜率为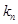 ,则
,则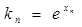 .
.
∴直线 的方程为
的方程为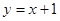 .令
.令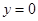 ,得
,得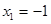 ,
1分
,
1分
∴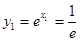 ,
∴
,
∴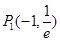 . ∴
. ∴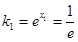 .
.
∴直线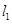 的方程为
的方程为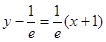 .令
.令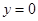 ,得
,得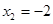 .
2分
.
2分
一般地,直线 的方程为
的方程为 ,
,
由于点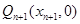 在直线
在直线 上,∴
上,∴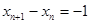 .
3分
.
3分
∴数列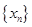 是首项为
是首项为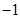 ,公差为
,公差为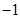 的等差数列.∴
的等差数列.∴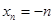 .
4分
.
4分
(2)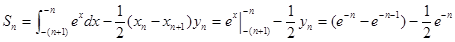
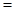
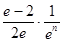 .
6分
.
6分
(3)证明: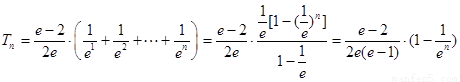 , 8分
, 8分
∴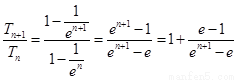 ,
,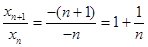 .
.
要证明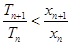 ,只要证明
,只要证明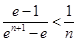 ,即只要证明
,即只要证明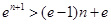 . 9分
. 9分
证法1:(数学归纳法)
①当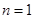 时,显然
时,显然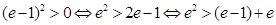 成立;
成立;
②假设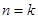 时,
时, 成立,则当
成立,则当 时,
时,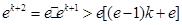 ,
,
而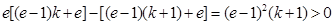 ,
,
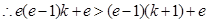 ,
,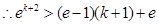 ,
,
 时,也成立,由①②知不等式
时,也成立,由①②知不等式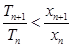 对一切
对一切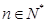 都成立.
14分
都成立.
14分
证法2: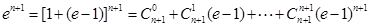
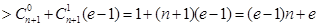 .
.
所以不等式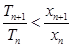 对一切
对一切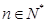 都成立.
14分
都成立.
14分
证法3:令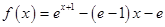 ,则
,则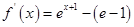 ,
,
当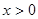 时,
时, 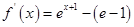
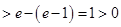 ,
,
∴函数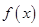 在
在 上单调递增. ∴当
上单调递增. ∴当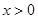 时,
时, 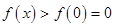 .
.
∵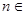 N
N ,
∴
,
∴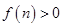 , 即
, 即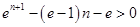 .∴
.∴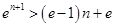 .
.
∴不等式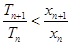 对一切
对一切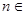 N
N 都成立.
14分
都成立.
14分
考点:1、利用导数求切线方程;2、数列的运算;3、定积分计算图形面积.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源:导学大课堂必修四数学苏教版 苏教版 题型:044
在日常生活中我们知道,如果今天是星期一,那么过7天后的那一天是星期一,再过7天后的那一天仍然是星期一,如此这般,一遍一遍地循环变化,周而复始.这就是人们常谈的周期性.然而在数学上也能反映出美丽的规律曲线,如下图A、B、C.
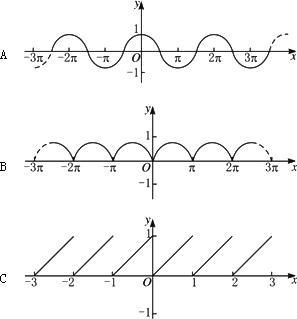
请问:这些图象都呈现出怎样的变化规律?
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试、文科数学(湖南卷) 题型:044
为了考察冰川的融化状况,一支科考队在某冰川山上相距8 Km的A、B两点各建一个考察基地,视冰川面为平面形,以过A、B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(下图).考察范围到A、B两点的距离之和不超过10 Km的区域.
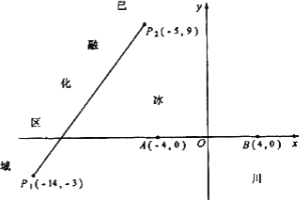
(Ⅰ)求考察区域边界曲线的方程:
(Ⅱ)如图所示,设线段P1P2是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2 km,以后每年移动的距离为前一年的2倍.问:经过多长时间,点A恰好在冰川边界线上?
查看答案和解析>>
科目:高中数学 来源:湖南省高考真题 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:

(1)建立适当的坐标系,求曲线E的方程;
(2)设点K是曲线E上的一动点,求线段KA中点的轨迹方程;
(3)若F(1,![]() )是曲线E上的一点,设M、N是曲线E上不同的两点,直线FM和FN的倾斜角互补,试判断直线MN的斜率是否为定值?如果是,求出这个定值;如果不是,请说明理由.
)是曲线E上的一点,设M、N是曲线E上不同的两点,直线FM和FN的倾斜角互补,试判断直线MN的斜率是否为定值?如果是,求出这个定值;如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com