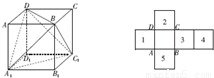
分析:①与AD
1成60°角的面对角线的条数是8条,由棱柱的面对角线的夹角与位置关系进行判断;
②直线AA
1与平面A
1BD所成角的余弦值是
,求出线面角时行验证;
③从8个顶点中取四个点可组成 10 个正三棱锥,所组成的正三棱锥只能是三个面对角线组成的三角形为底面,有此特征即可验证;
④点A
1到直线BC
1的距离是
,求出点到线的距离时行验证.
解答:解:

①与AD
1成60°角的面对角线的条数是8条,由图形中可以看出除了其所在面以及平行的两个面外的四个表面中每个面的两条面对角线都与AD
1成60°角,恰有8条,故命题正确;
②直线AA
1与平面A
1BD所成角的余弦值是
,取底面ABCD中点O,可证得∠AA
1O即是线AA
1与平面A
1BD所成角,求得线面角的余弦值为
,故此命题不对;
③从8个顶点中取四个点可组成 10 个正三棱锥,由图形的结构知,以8个顶点为顶点,以此点出发的三条侧棱为侧棱可以 组成8个正三棱锥,由面对角线可以组成两个正四面体,共可以组成10个正三棱锥,故命题正确;
④点A
1到直线BC
1的距离是
,由于A
1B
1⊥侧面B
1C,且侧面是正方形,连接B
1C与BC
1交于一点M,由正方形的性质知,此两直线垂直,连接A
1M其长度即为所求点A
1到直线BC
1的距离,利用勾股定理解得,其长度是
,故命题不正确.
综上知①③正确
故答案为:①③.
点评:本题考查棱柱的结构特征,解题的关键是对棱柱中的点线面的位置关系有着很好的理解,空间想像力比较强,才可以迅速找到判断问题的思路,代且图象研究此类问题是一个较好的办法.

 ①与AD1成60°角的面对角线的条数是8条,由图形中可以看出除了其所在面以及平行的两个面外的四个表面中每个面的两条面对角线都与AD1成60°角,恰有8条,故命题正确;
①与AD1成60°角的面对角线的条数是8条,由图形中可以看出除了其所在面以及平行的两个面外的四个表面中每个面的两条面对角线都与AD1成60°角,恰有8条,故命题正确;

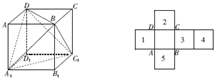 (2011•安徽模拟)下面关于棱长为1的正方体ABCD-A1B1C1D1叙述正确的是
(2011•安徽模拟)下面关于棱长为1的正方体ABCD-A1B1C1D1叙述正确的是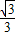 ;
;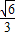 .
. 内的情况有4种.
内的情况有4种.