
(本小题满分11分) 已知函数 ,其中
,其中 .
.
(1) 当 时,求
时,求 的单调区间;
的单调区间;
(2) 证明:对任意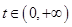 ,
, 在区间
在区间 内存在零点.
内存在零点.
解:(1) (I) 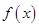 的单调增区间是
的单调增区间是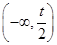 ,
, ,单调减区间是
,单调减区间是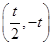 .
.
(II) 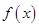 的单调增区间是
的单调增区间是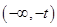 ,
,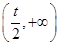 ,单调减区间是
,单调减区间是 .
.
(2) (I)对任意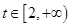 ,
,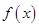 在区间
在区间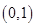 内存在零点.
内存在零点.
(II)对任意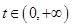 ,
,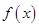 在区间
在区间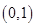 内存在零点.
内存在零点.
【解析】本试题主要是考查了函数的零点的概念,以及函数的单调区间的求解的综合运用。
(1)利用导数的思想,先分析函数的导数,然后确定参数t的值对于单调区间的影响,分类讨论得到结论。
(2)由上可知,当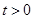 时,
时,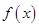 在
在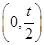 内单调递减,在
内单调递减,在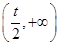 内单调递增.需要讨论
内单调递增.需要讨论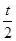 与讨论的区间
与讨论的区间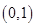 的相互位置关系,然后得到结论。
的相互位置关系,然后得到结论。
解:(1) 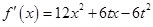 ,令
,令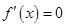 ,解得
,解得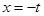 或
或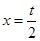 .…………1分
.…………1分
因为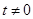 ,所以要分为
,所以要分为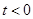 和
和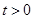 讨论.
讨论.
(I) 若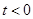 ,则
,则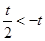 .
.
当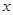 变化时,
变化时,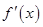 ,
,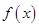 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
单调递增 |
单调递减 |
单调递增 |
所以,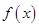 的单调增区间是
的单调增区间是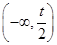 ,
, ,单调减区间是
,单调减区间是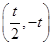 .…………3分
.…………3分
(II) 若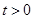 ,则
,则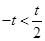 .
.
当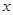 变化时,
变化时,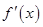 ,
,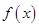 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
单调递增 |
单调递减 |
单调递增 |
所以,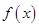 的单调增区间是
的单调增区间是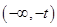 ,
,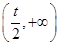 ,单调减区间是
,单调减区间是 .…………5分
.…………5分
(2) 由(Ⅱ)可知,当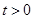 时,
时,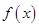 在
在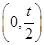 内单调递减,在
内单调递减,在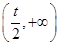 内单调递增.需要讨论
内单调递增.需要讨论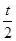 与讨论的区间
与讨论的区间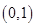 的相互位置关系.
的相互位置关系.
(I) 当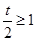 ,即
,即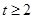 时,
时,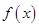 在
在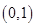 内单调递减,
内单调递减,
因为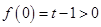 ,
,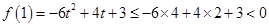 ,
,
所以对任意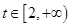 ,
,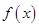 在区间
在区间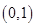 内存在零点.…………7分
内存在零点.…………7分
(II) 当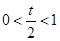 ,即
,即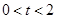 时,
时,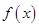 在
在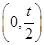 内单调递减,在
内单调递减,在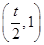 内单调递增.
内单调递增.
若 ,
,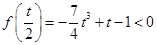 ,
,
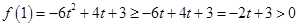 .
.
所以对任意 ,
,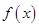 在区间
在区间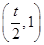 内存在零点.
内存在零点.
若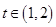 ,
,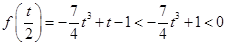 ,
,
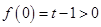 .
.
所以对任意 ,
,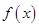 在区间
在区间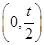 内存在零点.
内存在零点.
所以对任意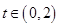 ,
,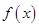 在区间
在区间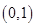 内存在零点.
内存在零点.
综上,对任意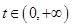 ,
,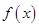 在区间
在区间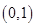 内存在零点.…………11分
内存在零点.…………11分


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2011-2012学年福建省高二上学期期中考试理科数学 题型:解答题
(本小题满分11分)
已知a、b、c为三角形ABC中角A、B、C的对边,且
 ,求这个三角形的最大内角.
,求这个三角形的最大内角.
查看答案和解析>>
科目:高中数学 来源:2010年陕西省西安市铁一中高二下学期期中考试数学(理) 题型:解答题
(本小题满分11分)已知,
 ;
;
(1)试由此归纳出当 时相应的不等式;
时相应的不等式;
(2)试用数学归纳法证明你在第(1)小题得到的不等式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com