分析:(I)以点B为坐标原点,分别以直线BA、BC、BB1为x轴、y轴建立空间直角坐标系Oxyz,设AB=2,欲证PA⊥B1C,只需它们对应的坐标,计算它们的数量积,使数量积为零即可;
(II)先求出平面B1C的一个法向量,先求直线PA与法向量的夹角的余弦值然后得到直线与平面所成角的正弦值,可求出k的值,最后求出平面BPC的一个法向量,根据两法向量的夹角的余弦值求出二面角A-PC-B的余弦值.
解答:解:以点B为坐标原点,分别以直线BA、BC、BB
1为x轴、y轴建立空间直角坐标系Oxyz.
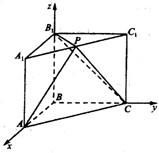
(I)设AB=2,则AB=BC=PA=2
根据题意得:
A(2,0,0),c(0,2,0),B1(0,0,),P(1,1,)所以
=(-1.1,),=(0,2,-).
∵
•=0+2-2=0,∴PA⊥B
1C.
(II)设AB=2,则
AP=,
根据题意:A(2,0,0),C(0,2,0),
又因为
A1P=A1C1=,
所以
AA1==,
∴
B1(0,0,),
∴
P(1,1,)=(-1,1,),
∵AB⊥平面B
1C,
所以由题意得
|cos<,>|=,
即
||=,即
=,
∵k>0,解得k=
.
即
k=时,直线PA与平面BB
1C
1C所成的角的正弦值为
.(8分)
∵B
1P⊥面APC,∴平面APC的法向量
=(1,0,0).
设平面BPC的一个法向量为
=(x,y,z),
∵
=(0,2,0),(1,1,)由
,得
,
∴
cos<,>=|=||=所以此时二面角A-PC-B的余弦值是
.(12分)
点评:本题主要考查了空间中直线与直线之间的位置关系,以及利用向量法度量二面角的大小,属于基础题.

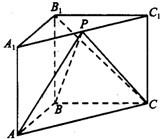 如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,P为A1C1的中点,AB=BC=kPA.
如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,P为A1C1的中点,AB=BC=kPA.


 阅读快车系列答案
阅读快车系列答案



