练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
        如图，已知三角形PAQ顶点P（-3，0），点A在y轴上，点Q在x轴正半轴上，。

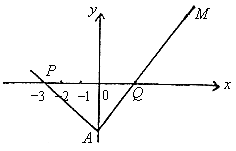
    （I）　　　　　　　　  当点A在y轴上移动时，求动点M的轨迹E的方程；

     

    （II）设直线与轨迹E交于B、C两点，点D（1，0），若∠BDC为钝角，求k的取值范围。

     

    答案：
    解析：

    		答案：解：（I）设

        则

        又

        又

       

        由<1><2>

        （II）设

       

        ∵∠BDC为钝角，

       

       

        由消去y得：

       

        则

       

        <4><5>代入<3>得：，此时

        ，∴k的范围是

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

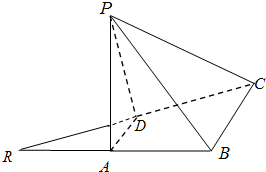    精英家教网如图，已知等腰直角三角形RBC，其中∠RBC=90°，RB=BC=2．点A、D分别是RB、RC的中点，现将△RAD沿着边AD折起到△PAD位置，使PA⊥AB，连接PB、PC．
    （1）求证：BC⊥PB；
    （2）求二面角A-CD-P的平面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2009•河西区二模）如图，已知三棱锥P-ABC中，PA⊥面ABC，其中正视图为Rt△PAC，AC=2
    		6
    ，PA=4，俯视图也为直角三角形，另一直角边长为2
    		2
    ．
    （Ⅰ）画出侧视图并求侧视图的面积；
    （Ⅱ）证明面PAC⊥面PAB；
    （Ⅲ）求直线PC与底面ABC所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•宝鸡模拟）如图，已知PA⊥平面ABC，且PA=
    		2
    ，等腰直角三角形ABC中，AB=BC=1，AB⊥BC，AD⊥PB于D，AE⊥PC于E．
    （1）求证：PC⊥平面ADE；
    （2）求点D到平面ABC的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•宝鸡模拟）如图，已知PA⊥平面ABC，且PA=
    		2
    ，等腰直角三角形ABC中，AB=BC=1，AB⊥BC，AD⊥PB于D，AE⊥PC于E．
    （1）求证：PC⊥平面ADE；
    （2）求直线AB与平面ADE所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知三棱锥P-ABC的侧面PAC是底角为45°的等腰三角形，PA=PC，且该侧面垂直于底面，∠ACB=90°，AB=10，BC=6，B1C1=3．
    （1）求证：二面角A-PB-C是直二面角；
    （2）求二面角P-AB-C的正切值；
    （3）若该三棱锥被平行于底面的平面所截，得到一个几何体ABC-A1B1C1，求几何体ABC-A1B1C1的侧面积．

    查看答案和解析>>

    同步练习册答案