在实数集R中,我们定义的大小关系“>”为全体实数排了一个“序”.类似地,我们在复数集C上也可以定义一个称为“序”的关系,记为“>”.定义如下:对于任意两个复数z1=a1+b1i,z2=a2+b2i(a1,b1,a2,b2∈R,i为虚数单位),“z1>z2”当且仅当“a1>a2”或“a1=a2且b1>b2”.下面命题为假命题的是( )
A.1>i>0
B.若z1>z2,z2>z3,则z1>z3
C.若z1>z2,则对于任意z∈C,z1+z>z2+z
D.对于复数z>0,若z1>z2,则z•z1>z•z2
【答案】
分析:根据复数集C上定义的“序”的关系,对A,B,C,D逐个判断,即可得到答案.
解答:解:设两个复数z
1=a
1+b
1i,z
2=a
2+b
2i(a
1,b
1,a
2,b
2∈R,i为虚数单位),
∵“a
1>a
2”或“a
1=a
2且b
1>b
2”?“z
1>z
2”,
∴对于A,z
1=1+0i,z
2=0+i,z
3=0+0i,
显然1=
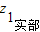
>

=
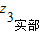
=0,1=

>

=0,
∴A正确;
对于B,同理可得当z
1>z
2,z
2>z
3时,z
1>z
3,故B正确;
对于C,∵z
1>z
2,
∴
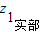
>

或
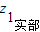
=

,
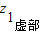
>

,
若
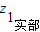
>

,(z
1+z)
实部>(z
2+z)
实部;
若
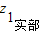
=

,
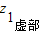
>

,则(z
1+z)
实部=(z
2+z)
实部,(z
1+z)
虚部>(z
2+z)
虚部,
故C正确;
对于D,按照新“序”的定义,复数z>0,不妨设z=i,z
1=1+i,z
2=1-i,显然z
1>z
2,
而z•z
1=i•(1+i)=-1+i,
z•z
2=i•(1-i)=1-i,
显然z•z
1<z•z
2,
故选D.
点评:本题考查复数的基本概念,理解复数集C上定义的“序”及其应用是关键,也是难点,考查分析与运算能力,属于中档题.

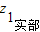 >
> =
=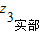 =0,1=
=0,1= >
> =0,
=0,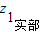 >
> 或
或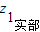 =
= ,
,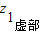 >
> ,
,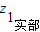 >
> ,(z1+z)实部>(z2+z)实部;
,(z1+z)实部>(z2+z)实部;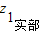 =
= ,
,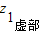 >
> ,则(z1+z)实部=(z2+z)实部,(z1+z)虚部>(z2+z)虚部,
,则(z1+z)实部=(z2+z)实部,(z1+z)虚部>(z2+z)虚部,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案