
【题目】已知由甲、乙两位男生和丙、丁两位女生组成的四人冲关小组,参加由安徽卫视推出的大型户外竞技类活动《男生女生向前冲》.活动共有四关,若四关都闯过,则闯关成功,否则落水失败.设男生闯过一至四关的概率依次是![]() ,女生闯过一至四关的概率依次是
,女生闯过一至四关的概率依次是![]() .
.
(Ⅰ)求男生甲闯关失败的概率;
(Ⅱ)设![]() 表示四人冲关小组闯关成功的人数,求随机变量
表示四人冲关小组闯关成功的人数,求随机变量![]() 的分布列和期望.
的分布列和期望.
科目:高中数学 来源: 题型:
【题目】设直线![]() 经过点
经过点![]() 倾斜角为
倾斜角为![]() .(10分).
.(10分).
(1)写出直线![]() 的参数方程
的参数方程
(2)求直线![]() 与直线
与直线![]() 的交点到点
的交点到点![]() 的距离
的距离
(3)设![]() 与圆
与圆![]()
![]() 相交于两点
相交于两点![]() ,求点
,求点![]() 到
到![]() 两点的距离的和与积。
两点的距离的和与积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东莞市某高级中学在今年4月份安装了一批空调,关于这批空调的使用年限![]() (单位:年,
(单位:年, ![]() )和所支出的维护费用
)和所支出的维护费用![]() (单位:万元)厂家提供的统计资料如下:
(单位:万元)厂家提供的统计资料如下:

(1)请根据以上数据,用最小二乘法原理求出维护费用![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若规定当维护费用![]() 超过13.1万元时,该批空调必须报废,试根据(1)的结论预测该批空调使用年限的最大值.
超过13.1万元时,该批空调必须报废,试根据(1)的结论预测该批空调使用年限的最大值.
参考公式:最小二乘估计线性回归方程![]() 中系数计算公式:
中系数计算公式:
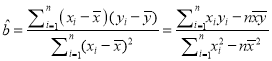 ,
, ![]() ,其中
,其中![]() 表示样本均值.
表示样本均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com