
����Ŀ����ݸ��ij����ѧ�ڽ���4�·ݰ�װ��һ���յ������������յ���ʹ������![]() ����λ���꣬
����λ���꣬ ![]() ������֧����ά������
������֧����ά������![]() ����λ����Ԫ�������ṩ��ͳ���������£�
����λ����Ԫ�������ṩ��ͳ���������£�

��1��������������ݣ�����С���˷�ԭ�����ά������![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
��2�����涨��ά������![]() ����13.1��Ԫʱ�������յ����뱨�ϣ��Ը��ݣ�1���Ľ���Ԥ������յ�ʹ���������ֵ.
����13.1��Ԫʱ�������յ����뱨�ϣ��Ը��ݣ�1���Ľ���Ԥ������յ�ʹ���������ֵ.
�ο���ʽ����С���˹������Իع鷽��![]() ��ϵ�����㹫ʽ��
��ϵ�����㹫ʽ��
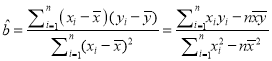 ��
�� ![]() ������
������![]() ��ʾ������ֵ.
��ʾ������ֵ.

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C��Ӧ�ı߷ֱ���a��b��c��C= ![]() ����sinB=2sinAcos��A+B����
����sinB=2sinAcos��A+B����
��1��֤����b2=2a2��
��2������ABC�������1�����c��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
�� ![]() ������������
������������![]() ��
��![]() Ϊ��Ȼ�����ĵף�.
Ϊ��Ȼ�����ĵף�.
��1�����ۺ���![]() �ļ�ֵ��ĸ�����
�ļ�ֵ��ĸ�����
��2��������ʽ![]() ��
��![]() ���������ʵ����
���������ʵ����![]() ȡֵ��Χ.
ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ɼס�����λ�����ͱ�������λŮ����ɵ����˳��С�飬�μ��ɰ��������Ƴ��Ĵ��ͻ��⾺����������Ů����ǰ�塷.������Ĺأ����Ĺض��������سɹ���������ˮʧ��.����������һ���Ĺصĸ���������![]() ��Ů������һ���Ĺصĸ���������
��Ů������һ���Ĺصĸ���������![]() .
.
�����������״���ʧ�ܵĸ��ʣ�
������![]() ��ʾ���˳��С�鴳�سɹ������������������
��ʾ���˳��С�鴳�سɹ������������������![]() �ķֲ��к�����.
�ķֲ��к�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C���Եı߷ֱ�Ϊa��b��c�������� ![]() acosC��csinA=0��
acosC��csinA=0��
��1�����C�Ĵ�С��
��2����֪b=4����ABC�����Ϊ6 ![]() ����߳�c��ֵ��
����߳�c��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У��ڽ�A��B��C�ĶԱ߷ֱ�Ϊa��b��c����֪ ![]()
��1���� ![]() ��ֵ��
��ֵ��
��2���� ![]() ��b=2�����ABC�����S��
��b=2�����ABC�����S��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����������ͼ����ͼ����ü���������Ϊ�� ��
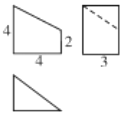
A. 18 B. 20 C. 24 D. 12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=sin��x���գ����� ![]() f��x��dx=0������f��x����ͼ���һ���Գ����ǣ� ��
f��x��dx=0������f��x����ͼ���һ���Գ����ǣ� ��
A.x= ![]()
B.x= ![]()
C.x= ![]()
D.x= ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��1979�꣬��������ʿ���й��Ƽ���ѧ��������һ����Ȥ�⣺5ֻ���ӷ�һ�����ӣ���ôҲ���ֳܷ�5�ȷݣ�ֻ����ȥ˯�������ڶ����ٷ֣�ҹ��1ֻ����͵͵���������ȳԵ�һ�����ӣ�Ȼ����ֳ�5�ȷݣ������Լ���һ�ݾ�ȥ˯���ˣ���2ֻ����������������ʣ������ӳԵ�һ����Ҳ�����ӷֳ�5�ȷݣ������Լ���һ��˯��ȥ�ˣ��Ժ��3ֻ���Ӷ��Ⱥ��մ˰������ʣ���������ж��ٸ����ӣ��������ʣ�¶��ٸ����ӣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com