练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在ABC中，内角A，B，C的对边分别为a，b，c，已知
    （1）求 的值；
    （2）若 ，b=2，求△ABC的面积S．

    【答案】
    （1）解：由正弦定理设

    则 = = =

    整理求得sin（A+B）=2sin（B+C）

    又A+B+C=π

    ∴sinC=2sinA，即 =2


    （2）解：由余弦定理可知cosB= = ①

    由（1）可知 = =2②

    再由b=2，①②联立求得c=2，a=1

    sinB= =

    ∴S= acsinB=


    【解析】（1）利用正弦定理把题设等式中的边转化成角的正弦，整理后可求得sinC和sinA的关系式，则 的值可得．（2）先通过余弦定理可求得a和c的关系式，同时利用（1）中的结论和正弦定理求得a和c的另一关系式，最后联立求得a和c，利用三角形面积公式即可求得答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】《中国诗词大会》是中央电视台最近推出的一档有重大影响力的大型电视文化节目，今年两会期间，教育部部长陈宝生答记者问时就给予其高度评价．基于这样的背景，山东某中学积极响应，也举行了一次诗词竞赛．组委会在竞赛后，从中抽取了部分选手的成绩（百分制），作为样本进行统计，作出了图1的频率分布直方图和图2的茎叶图（但中间三行污损，看不清数据）．

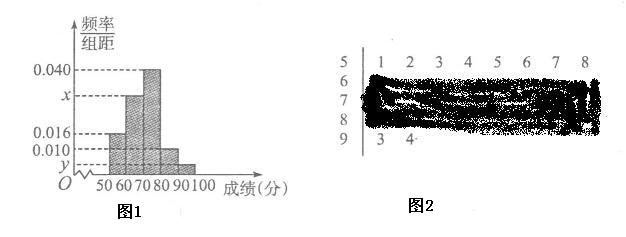
    （I）求样本容量和频率分布直方图中的，的值；

    （II）分数在[80，90）的学生中，男生有2人，现从该组抽取三人“座谈”，写出基本事件空间并求至少有两名女生的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知正数x、y满足xy=x+y+3．
    （1）求xy的范围；
    （2）求x+y的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】东莞市某高级中学在今年4月份安装了一批空调，关于这批空调的使用年限（单位：年， ）和所支出的维护费用（单位：万元）厂家提供的统计资料如下：

    （1）请根据以上数据，用最小二乘法原理求出维护费用关于的线性回归方程；

    （2）若规定当维护费用超过13.1万元时，该批空调必须报废，试根据（1）的结论预测该批空调使用年限的最大值.

    参考公式：最小二乘估计线性回归方程中系数计算公式：

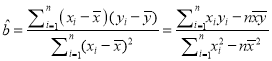    ， ，其中表示样本均值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直角坐标系中，圆与轴负半轴交于点，过点的直线,分别与圆交于,两点．

    （Ⅰ）若,，求的面积；

    （Ⅱ）若直线过点，证明：为定值，并求此定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}中，a1=1，a3=﹣3．
    （1）求数列{an}的通项公式；
    （2）若数列{an}的前k项和Sk=﹣35，求k的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， 为实常数．

    (Ⅰ)设，当时，求函数的单调区间；

    (Ⅱ)当时，直线、与函数、的图象一共有四个不同的交点，且以此四点为顶点的四边形恰为平行四边形．

    求证： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，圆C：x2+y2﹣8y+12=0，直线l：ax+y+2a=0．
    （1）当a为何值时，直线l与圆C相切；
    （2）当直线l与圆C相交于A、B两点，且AB=2 时，求直线l的方程．

    查看答案和解析>>

    同步练习册答案