
【题目】已知函数![]() (
(![]() ,
, ![]() 为常数),函数
为常数),函数![]() (
(![]() 为自然对数的底).
为自然对数的底).
(1)讨论函数![]() 的极值点的个数;
的极值点的个数;
(2)若不等式![]() 对
对![]() 恒成立,求实数的
恒成立,求实数的![]() 取值范围.
取值范围.
【答案】(1)详见解析(2)![]()
【解析】试题分析:(1)求得![]()
![]()
![]() ,分三种情况讨论,分别研究函数的单调性进而可得函数极值点的个数;(2)不等式
,分三种情况讨论,分别研究函数的单调性进而可得函数极值点的个数;(2)不等式![]() 对
对![]() 恒成立,等价于
恒成立,等价于![]() 只需研究函数
只需研究函数![]() 的最小值不小于零即可.
的最小值不小于零即可.
试题解析:(1)![]()
![]()
![]() ,
,
由![]() 得:
得: ![]() ,记
,记![]() ,则
,则![]() ,
,
由![]() 得
得![]() ,且
,且![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
,
所以当![]() 时,
时, ![]() 取得最大值
取得最大值![]() ,又
,又![]() ,
,
(i)当![]() 时,
时, ![]() 恒成立,函数
恒成立,函数![]() 无极值点;
无极值点;
(ii)当![]() 时,
时, ![]() 有两个解
有两个解![]() ,
, ![]() ,且
,且![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,所以函数
,所以函数![]() 有两个极值点;
有两个极值点;
(iii)当![]() 时,方程
时,方程![]() 有一个解
有一个解![]() ,且
,且![]() 时
时![]() ,
, ![]() 时,
时, ![]() ,所以函数
,所以函数![]() 有一个极值点;
有一个极值点;
(2)记![]()
![]()
![]() ,
,
由![]() ,
,
![]() ,
, ![]() ,
,
由![]() ,
,
又当![]() ,
, ![]() 时,
时, ![]()
![]() ,
,
![]() ,
, ![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
综上实数![]() 的取值范围是
的取值范围是![]() .
.
【方法点晴】本题主要考查利用导数求函数的最值以及不等式恒成立问题,属于难题.不等式恒成立问题常见方法:① 分离参数![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立(
恒成立(![]() 即可);② 数形结合(
即可);② 数形结合(![]() 图象在
图象在![]() 上方即可);③ 讨论最值
上方即可);③ 讨论最值![]() 或
或![]() 恒成立;④ 讨论参数.本题是利用方法 ③ 求得
恒成立;④ 讨论参数.本题是利用方法 ③ 求得![]() 的范围的.
的范围的.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】已知{an}是公差为1的等差数列,a1 , a5 , a25成等比数列.
(1)求数列{an}的通项公式;
(2)设bn= ![]() 3+an , 求数列{bn}的前n项和Tn .
3+an , 求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东莞市某高级中学在今年4月份安装了一批空调,关于这批空调的使用年限![]() (单位:年,
(单位:年, ![]() )和所支出的维护费用
)和所支出的维护费用![]() (单位:万元)厂家提供的统计资料如下:
(单位:万元)厂家提供的统计资料如下:

(1)请根据以上数据,用最小二乘法原理求出维护费用![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若规定当维护费用![]() 超过13.1万元时,该批空调必须报废,试根据(1)的结论预测该批空调使用年限的最大值.
超过13.1万元时,该批空调必须报废,试根据(1)的结论预测该批空调使用年限的最大值.
参考公式:最小二乘估计线性回归方程![]() 中系数计算公式:
中系数计算公式:
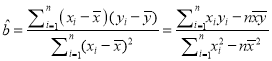 ,
, ![]() ,其中
,其中![]() 表示样本均值.
表示样本均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗![]() 原料1千克、
原料1千克、![]() 原料2千克;生产乙产品1桶需耗
原料2千克;生产乙产品1桶需耗![]() 原料2千克,
原料2千克, ![]() 原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗
原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗![]() 原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是__________元.
原料都不超过12千克.通过合理安排生产计划,从每天生产的甲、乙两种产品中,公司共可获得的最大利润是__________元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com