
 、
、 ,科目B的正考和补考成绩合格的概率均为
,科目B的正考和补考成绩合格的概率均为 ,假设各次考试成绩合格与否均互不影响.
,假设各次考试成绩合格与否均互不影响. =
= ;
;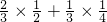 =
= ;P(ξ=3)=
;P(ξ=3)=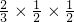 +
+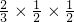 +
+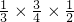 =
=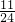 ;
;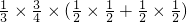 =
=
| P | 2 | 3 | 4 |
| ξ |  | 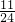 |  |
 +3×
+3×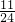 +4×
+4× =
=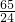


科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 3 |
| 4 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试理科数学(福建卷) 题型:选择题
(本小题满分12分)
某项考试按科目A、科目B依次进行,只有当科目A成绩合格时,才可继续参加科目B的考试。已知每个科目只允许有一次补考机会,两个科目成绩均合格方可获得证书。现某人参加这项考试,科目A每次考试成绩合格的概率均为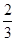 ,科目B每次考试成绩合格的概率均为
,科目B每次考试成绩合格的概率均为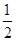 ,假设各次考试成绩合格与否均互不影响。
,假设各次考试成绩合格与否均互不影响。
(Ⅰ)求他不需要补考就可获得证书的概率;
(Ⅱ)在这项考试过程中,假设他不放弃所有的考试机会,记他参加考试的次数为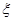 ,求
,求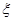 的数学期望E
的数学期望E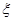 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com