
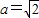 ”,q:“直线x+y=0与圆x2+(y-a)2=1相切”,则p是q的( )
”,q:“直线x+y=0与圆x2+(y-a)2=1相切”,则p是q的( )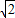 时,把a的值代入圆的方程中,找出圆心坐标和圆的半径,根据点到直线的距离公式求出圆心到直线x+y=0的距离d,发现d等于圆的半径r,进而得到直线与圆的位置关系是相切;而当直线x+y=0与圆相切时,由圆心坐标和圆的半径,利用点到直线的距离公式表示出圆心(0,a)到直线x+y=0的距离d,让d等于圆的半径1列出关于a的方程,求出方程的解即可得到a的值为两个值,综上,得到p是q的充分非必要条件.
时,把a的值代入圆的方程中,找出圆心坐标和圆的半径,根据点到直线的距离公式求出圆心到直线x+y=0的距离d,发现d等于圆的半径r,进而得到直线与圆的位置关系是相切;而当直线x+y=0与圆相切时,由圆心坐标和圆的半径,利用点到直线的距离公式表示出圆心(0,a)到直线x+y=0的距离d,让d等于圆的半径1列出关于a的方程,求出方程的解即可得到a的值为两个值,综上,得到p是q的充分非必要条件.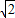 时,圆的方程为:x2+(y-
时,圆的方程为:x2+(y- )2=1,
)2=1,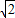 ),半径r=1,
),半径r=1,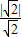 =1=r,
=1=r,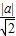 =1,解得a=±
=1,解得a=±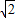 ,
,

 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:
|
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com