
【题目】已知函数f(x)=sin2xsin2x.
(1)讨论f(x)在区间(0,π)的单调性;
(2)证明:![]() ;
;
(3)设n∈N*,证明:sin2xsin22xsin24x…sin22nx≤![]() .
.
【答案】(1)当![]() 时,
时,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() 单调递增.(2)证明见解析;(3)证明见解析.
单调递增.(2)证明见解析;(3)证明见解析.
【解析】
(1)首先求得导函数的解析式,然后由导函数的零点确定其在各个区间上的符号,最后确定原函数的单调性即可;
(2)首先确定函数的周期性,然后结合(1)中的结论确定函数在一个周期内的最大值和最小值即可证得题中的不等式;
(3)对所给的不等式左侧进行恒等变形可得![]() ,然后结合(2)的结论和三角函数的有界性进行放缩即可证得题中的不等式.
,然后结合(2)的结论和三角函数的有界性进行放缩即可证得题中的不等式.
(1)由函数的解析式可得:![]() ,则:
,则:
![]()
![]()
![]()
![]() ,
,
![]() 在
在![]() 上的根为:
上的根为:![]() ,
,
当![]() 时,
时,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() 单调递减,
单调递减,
当![]() 时,
时,![]() 单调递增.
单调递增.
(2)注意到![]() ,
,
故函数![]() 是周期为
是周期为![]() 的函数,
的函数,
结合(1)的结论,计算可得:![]() ,
,
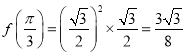 ,
,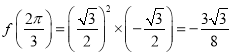 ,
,
据此可得:![]() ,
,![]() ,
,
即![]() .
.
(3)结合(2)的结论有:
![]()
![]()
![]()
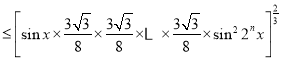
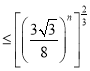
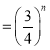 .
.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
【题目】设α,β是空间中的两个平面,l,m是两条直线,则使得α∥β成立的一个充分条件是( )
A.lα,mβ,l∥mB.l⊥m,l∥α,m⊥β
C.lα,mα,l∥β,m∥βD.l∥m,l⊥α,m⊥β
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层,上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块,下一层的第一环比上一层的最后一环多9块,向外每环依次也增加9块,已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)( )

A.3699块B.3474块C.3402块D.3339块
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 为参数
为参数![]() ,以坐标原点O为极点,以x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为
,以坐标原点O为极点,以x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
![]() 求直线l的普通方程及曲线C的直角坐标方程;
求直线l的普通方程及曲线C的直角坐标方程;
![]() 若直线l与曲线C交于A,B两点,求线段AB的中点P到坐标原点O的距离.
若直线l与曲线C交于A,B两点,求线段AB的中点P到坐标原点O的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的坐标方程为
的坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切.
相切.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() 、
、![]() 于原点
于原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,底面四边形ABCD是一个菱形,且∠ABC![]() ,AB=2,PA⊥平面ABCD.
,AB=2,PA⊥平面ABCD.
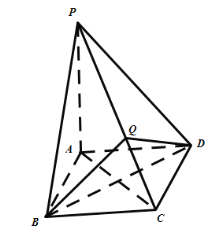
(1)若Q是线段PC上的任意一点,证明:平面PAC⊥平面QBD.
(2)当平面PBC与平面PDC所成的锐二面角的余弦值为![]() 时,求PA的长.
时,求PA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com