Question

已知a≥,函数f(x)=-a²x²+ax+c.

(1)证明：对任意x∈［0,1］,f(x)≤1的充要条件是c≤;

(2)已知关于x的实系数二次方程f(x)=0有两个实数根α、β，证明：|α|≤1且|β|≤1的充要条件是c≤a²-a.

Answer 1

分析：本题属于三个“二次”的问题，这类问题在解题时，首先要充分利用相应的二次函数的性质，特别是图象特征与单调性，由此可得解法.

解：(1)f(x)=-a²(x-)²+c+,∵a≥,∴0＜≤1,即∈(0,1]，

    当x∈［0,1］时，f(x)_max=f()=c+.

    充分性：∵c≤,

∴x∈［0,1］时,f(x)≤c+≤1,

∴f(x)≤1(x∈［0,1］).

    必要性：∵x∈［0,1］时，f(x)≤1,而∈(0,1),

∴f()=c+≤1,∴c≤.

(2)二次函数f(x)的图象开口向下，对称轴方程为x=,因为a≥,故∈(0,1)［-1,1］,

∴f(x)=0的两根α、β在［-1，1］内

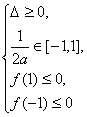
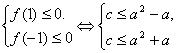
c≤a²-a,

∴|α|≤1且|β|≤1的充要条件是c≤a²-a.