
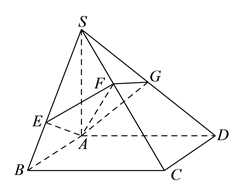
【题目】如图,已知矩形![]() ,过
,过![]() 作
作![]() 平面
平面![]() ,再过
,再过![]() 作
作![]() 于点
于点![]() ,过
,过![]() 作
作![]() 于点
于点![]() .
.
(Ⅰ)求证: ![]() .
.
(Ⅱ)若平面![]() 交
交![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)本题需经过多次线面垂直与线线垂直的转化:由![]() 平面
平面![]() ,得
,得![]() ,再得
,再得![]() 平面
平面![]() ,即得
,即得![]() ,可得
,可得![]() 平面
平面![]() ,即得
,即得![]() ,因此
,因此![]() 平面
平面![]() ,即得结论(2)本题仍需经过多次线面垂直与线线垂直的转化:由
,即得结论(2)本题仍需经过多次线面垂直与线线垂直的转化:由![]() 平面
平面![]() ,得
,得![]() ,再得
,再得![]() 平面
平面![]() ,即得
,即得![]() ,可得
,可得![]() 平面
平面![]() ,即得结论
,即得结论
试题解析:(Ⅰ)∵在矩形![]() 中,
中,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 点,
点,
![]() 、
、![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() ,
,
![]() 点,
点,
![]() 、
、![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() ,
,
![]() 点,
点,
![]() 、
、![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
(Ⅱ)∵在矩形![]() 中,
中,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 点,
点,
![]() 、
、![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 点,
点,
![]() 、
、![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行,需转化为证明线线平行.
(2)证明线面垂直,需转化为证明线线垂直.
(3)证明线线垂直,需转化为证明线面垂直.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
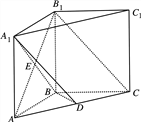
【题目】如图,在直三棱柱ABC—A1B1C1中,AB=BC=BB1, ![]() ,D为AC上的点,B1C∥平面A1BD;
,D为AC上的点,B1C∥平面A1BD;
(1)求证:BD⊥平面![]() ;
;
(2)若![]() 且
且![]() ,求三棱锥A-BCB1的体积.
,求三棱锥A-BCB1的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点E在⊙O上,C为 ![]() 的中点,过点C作直线CD⊥AE于D,连接AC、BC.
的中点,过点C作直线CD⊥AE于D,连接AC、BC.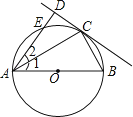
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC= ![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com