
【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
【答案】
(1)
∵关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根,
∴△=(2m+1)2﹣4×1×(m2﹣1)=4m+5>0,
解得:m>﹣ ![]() .
.
(2)
解:m=1,此时原方程为x2+3x=0,
即x(x+3)=0,
解得:x1=0,x2=﹣3.
【解析】(1)由方程有两个不相等的实数根即可得出△>0,代入数据即可得出关于m的一元一次不等式,解不等式即可得出结论;(2)结合(1)结论,令m=1,将m=1代入原方程,利用因式分解法解方程即可得出结论.
【考点精析】本题主要考查了因式分解法和求根公式的相关知识点,需要掌握已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势;根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】图1是某公交公司1路车从起点站A站途经B站和C站,最终到达终点站D站的格点站路线图.(8×8的格点图是由边长为1的小正方形组成)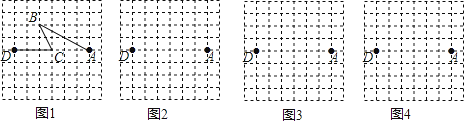
(1)求1路车从A站到D站所走的路程(精确到0.1);
(2)在图2、图3和图4的网格中各画出一种从A站到D站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球2次均未命中的概率为
,且乙投球2次均未命中的概率为![]() 。
。
(1)求乙投球的命中率![]() 。
。
(2)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时.生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,求在不超过600个工时的条件下,生产产品A和产品B的利润之和的最大值(元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙![]() 和点
和点![]() .过
.过![]() 作⊙
作⊙![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 且直线
且直线![]() 的方程为
的方程为![]() .
.
(1)求⊙![]() 的方程;
的方程;
(2)设![]() 为⊙
为⊙![]() 上任一点,过点
上任一点,过点![]() 向⊙
向⊙![]() 引切线,切点为
引切线,切点为![]() , 试探究:平面内是否存在一定点
, 试探究:平面内是否存在一定点![]() ,使得
,使得![]() 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com