
【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时.生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,求在不超过600个工时的条件下,生产产品A和产品B的利润之和的最大值(元).
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点E在⊙O上,C为 ![]() 的中点,过点C作直线CD⊥AE于D,连接AC、BC.
的中点,过点C作直线CD⊥AE于D,连接AC、BC.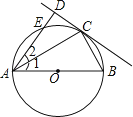
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC= ![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】林业部门要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组数据:
移植的棵数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
成活的棵数m | 865 | 1356 | 2220 | 3500 | 7056 | 13170 | 17580 | 26430 |
成活的频率 | 0.865 | 0.904 | 0.888 | 0.875 | 0.882 | 0.878 | 0.879 | 0.881 |
估计该种幼树在此条件下移植成活的概率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.
(1)求m的取值范围;
(2)写出一个满足条件的m的值,并求此时方程的根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左焦点为
的左焦点为![]() ,过点F做x轴的垂线交椭圆于A,B两点,且
,过点F做x轴的垂线交椭圆于A,B两点,且![]() .
.
(1)求椭圆C的标准方程:
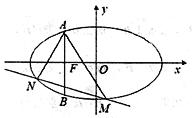
(2)若M,N为椭圆上异于点A的两点,且直线![]() 的倾斜角互补,问直线MN的斜率是否为定值?若是,求出这个定值;若不是,请说明理由.
的倾斜角互补,问直线MN的斜率是否为定值?若是,求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时.生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,求在不超过600个工时的条件下,生产产品A和产品B的利润之和的最大值(元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差d>0,则下列四个命题: ①数列{an}是递增数列;
②数列{nan}是递增数列;
③数列 ![]() 是递增数列;
是递增数列;
④数列{an+3nd}是递增数列;
其中正确命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知圆![]() 和直线
和直线![]() .
.
(Ⅰ)求![]() 的参数方程以及圆
的参数方程以及圆![]() 上距离直线
上距离直线![]() 最远的点
最远的点![]() 坐标;
坐标;
(Ⅱ)以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,将圆
轴正半轴为极轴建立极坐标系,将圆![]() 上除点
上除点![]() 以外所有点绕着
以外所有点绕着![]() 逆时针旋转
逆时针旋转![]() 得到曲线
得到曲线![]() ,求曲线
,求曲线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com