
【题目】已知曲线y=x3,求:
(1)曲线在点P(1,1)处的切线方程;
(2)过点P(1,0)的曲线的切线方程.
【答案】(1)3x-y-2=0;(2)3x-y-2=0
【解析】试题分析:(1)求出y的导数,求得切线的斜率,由点斜式方程可得切线的方程;
(2)设切点为(x0,y0),求得切线的斜率,由两点的斜率公式,解方程可得x0,进而得到切线的方程.
试题解析:
y′=3x2.
(1)当x=1时,y′=3,即在点P(1,1)处的切线的斜率为3,
∴切线方程为y-1=3(x-1),即3x-y-2=0.
(2)设切点坐标为(x0,y0),则过点P的切线的斜率为3x,
由直线的点斜式,得切线方程y-x=3x (x-x0),
即3xx-y-2x=0.
∵P(1,0)在切线上,∴3x-2x=0.
解之得x0=0或x0=![]() .
.
当x0=0时,切线方程为y=0.
当x0=![]() 时,切线方程为27x-4y-27=0.
时,切线方程为27x-4y-27=0.


科目:高中数学 来源: 题型:
【题目】图1是某公交公司1路车从起点站A站途经B站和C站,最终到达终点站D站的格点站路线图.(8×8的格点图是由边长为1的小正方形组成)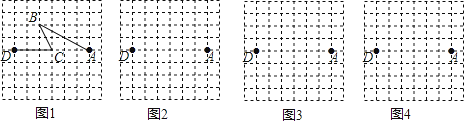
(1)求1路车从A站到D站所走的路程(精确到0.1);
(2)在图2、图3和图4的网格中各画出一种从A站到D站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时.生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,求在不超过600个工时的条件下,生产产品A和产品B的利润之和的最大值(元).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【河南省豫南九校(中原名校)2017届高三下学期质量考评八数学(文)】已知双曲线![]() 的左右两个顶点是
的左右两个顶点是![]() ,
, ![]() ,曲线
,曲线![]() 上的动点
上的动点![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与
与![]() 交于点
交于点![]() ,
,
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)点![]() ,轨迹
,轨迹![]() 上的点
上的点![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙![]() 和点
和点![]() .过
.过![]() 作⊙
作⊙![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 且直线
且直线![]() 的方程为
的方程为![]() .
.
(1)求⊙![]() 的方程;
的方程;
(2)设![]() 为⊙
为⊙![]() 上任一点,过点
上任一点,过点![]() 向⊙
向⊙![]() 引切线,切点为
引切线,切点为![]() , 试探究:平面内是否存在一定点
, 试探究:平面内是否存在一定点![]() ,使得
,使得![]() 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运行如图的程序,如果输入的m,n的值分别是24和15,记录输出的i和m的值.在平面直角坐标系xOy中,已知点A(i﹣4,m),圆C的圆心在直线l:y=2x﹣4上. 
(1)若圆C的半径为1,且圆心C在直线y=x﹣1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使∠OMA=90°,求圆C的半径r的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com