
在四棱锥 中,
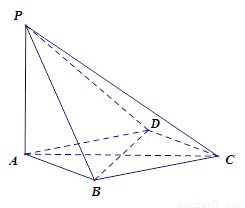
中,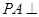 平面ABCD,底面ABCD是菱形,
平面ABCD,底面ABCD是菱形, ,
, .
.
(1)求证: 平面PAC;
平面PAC;
(2)若 ,求PB与AC所成角的余弦值;
,求PB与AC所成角的余弦值;
(3)若PA= ,求证:平面PBC⊥平面PDC
,求证:平面PBC⊥平面PDC
(1)由线线平行证得 (2)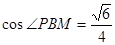 (3)求得
(3)求得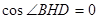 从而证明.
从而证明.
【解析】
试题分析:(1)证:因为四边形ABCD是菱形,
所以AC⊥BD.又因为PA⊥平面ABCD. 所以PA⊥BD,又AC∩PA=A
所以BD⊥平面PAC.
(2)解:过B作BM//AC交DA延长线于M,连接PM ∠PBM或其补角为所求
因为BM//AC
AM//BC 所以四边形MACB为平行四边形 所以BM=AC=2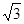 ,PB=PM=
,PB=PM= ,所以
,所以
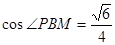 .
.
(3) 作BH⊥PC,连接HD
 PA⊥平面ABCD,AD="AB"
PA⊥平面ABCD,AD="AB"  PB=PD,又
PB=PD,又 CD="CB"
PC="PC"
CD="CB"
PC="PC"  △PBC≌△PDC
△PBC≌△PDC
 BH⊥PC
BH⊥PC
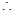 HD⊥PC 因此∠BHD为二面角B-PC-D的平面角
HD⊥PC 因此∠BHD为二面角B-PC-D的平面角
因为AP=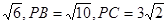 BC="2" 有BH=
BC="2" 有BH=
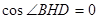 所以
面PBC⊥面PDC.
所以
面PBC⊥面PDC.
考点:直线与平面垂直的判定;点、线、面间的距离计算;用空间向量求直线间的夹角、距离.
点评:本小题主要考查空间线面关系的垂直关系的判断、异面直线所成的角、用空间向量的方法求解直线的
夹角、距离等问题,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算
求解能力.


科目:高中数学 来源:2011年江苏省普通高中招生考试数学 题型:解答题
(本小题满分14分)如图,在四棱锥 中,平面PAD⊥平面ABCD,
中,平面PAD⊥平面ABCD,
AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
求证:(1)直线EF‖平面PCD;
(2)平面BEF⊥平面PAD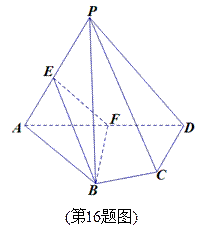
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省高三下学期模拟预测理科数学试卷(解析版) 题型:解答题
在四棱锥 中,
中, 平面
平面 ,底面
,底面 为矩形,
为矩形, .
.
(Ⅰ)当 时,求证:
时,求证: ;
;
(Ⅱ)若 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.

【解析】第一位女利用线面垂直的判定定理和性质定理得到。当a=1时,底面ABCD为正方形,

又因为 ,
, ………………2分
………………2分
又 ,得证。
,得证。
第二问,建立空间直角坐标系,则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分
设BQ=m,则Q(1,m,0)(0《m《a》
要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 时,存在点Q使得
时,存在点Q使得
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得
由此知道a=2, 设平面POQ的法向量为
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
则 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值为
解:(Ⅰ)当 时,底面ABCD为正方形,
时,底面ABCD为正方形,

又因为 ,
, 又
又
 ………………3分
………………3分
(Ⅱ) 因为AB,AD,AP两两垂直,分别以它们所在直线为X轴、Y轴、Z轴建立坐标系,如图所示,

则B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分
设BQ=m,则Q(1,m,0)(0《m《a》要使 ,只要
,只要
所以 ,即
,即 ………6分
………6分
由此可知 时,存在点Q使得
时,存在点Q使得
当且仅当m=a-m,即m=a/2时,BC边上有且只有一个点Q,使得 由此知道a=2,
由此知道a=2,
设平面POQ的法向量为
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
则 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值为
查看答案和解析>>
科目:高中数学 来源:2014届福建省高一下学期期中数学试卷(解析版) 题型:解答题
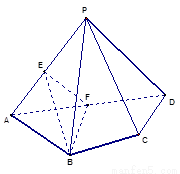
如图,在四棱锥 中,
中,
平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点求证:(1)直线EF//平面PCD;
(2)平面BEF⊥平面PAD
查看答案和解析>>
科目:高中数学 来源:2013届黑龙江省高二上学期期末考试理科数学 题型:解答题
(12分)在四棱锥 中,平面PAD⊥平面ABCD, AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
中,平面PAD⊥平面ABCD, AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
求证:(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD

查看答案和解析>>
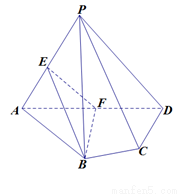
科目:高中数学 来源:2013届天津市高二上学期期中考试理科数学试卷 题型:解答题
如图,在四棱锥 中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
求证:(1)直线EF//平面PCD;(2)平面BEF⊥平面PAD

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com