解:(1)抛物线的焦点为(0,1),设椭圆的右焦点(c,0 ),则由题意可得
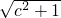
=

,
∴c=2,∴再由离心率可得 a=

,b=1,故椭圆的标准方程为
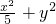
=1.
(2)设直线l的方程为 y=k(x+2),代入椭圆的方程化简可得 (1+5k
2)x
2+20k
2x-5=0,
∴x
1+x
2=
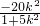
,x
1•x
2=
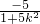
,
∴(

+

)=(x
1-m,y
1)+(x
2-m,y
2 )=(x
1+x
2-2m,y
1+y
2 ).
由(

+

)⊥

,可得 (

+

)•

=(x
1+x
2-2m,y
1+y
2 )•(x
2-x
1,y
2-y
1)
=(x
1+x
2-2m)(x
2-x
1)+(y
2+y
1)(y
2-y
1)=0,
化简可得 x
1+x
2-2m+k
2(x
1+x
2+4)=0,∴2m=4k
2-
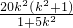
,
∴m=-
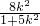
=-
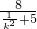
.∵k
2>0,∴0<
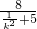
<

,
∴-

<m<0. 故m的取值范围是[-

,0).
分析:(1)根据题意设椭圆的右焦点(c,0 ),则由题意可得
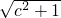
=

,求出c值,由离心率可得 a,求出b值,即得椭圆的标准方程.
(2)设直线l的方程为 y=k(x+2),代入椭圆的方程化简,把根与系数的关系代入(

+

)•

=0,解得 m=-
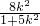
=-
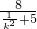
,再利用不等式的性质求出m的取值范围.
点评:本题考查求椭圆的标准方程,两个向量的数量积公式,不等式的性质,求出m=-
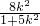
=-
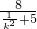
,是解题的关键,
属于中档题.

 ,离心率e=
,离心率e= ,过椭圆的左焦点厂做一条与坐标轴不垂直的直线L交椭圆于A,B两点.
,过椭圆的左焦点厂做一条与坐标轴不垂直的直线L交椭圆于A,B两点. +
+ )⊥
)⊥ ,求m的取值范围.
,求m的取值范围.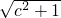 =
= ,
, ,b=1,故椭圆的标准方程为
,b=1,故椭圆的标准方程为 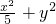 =1.
=1.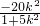 ,x1•x2=
,x1•x2=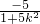 ,
, +
+ )=(x1-m,y1)+(x2-m,y2 )=(x1+x2-2m,y1+y2 ).
)=(x1-m,y1)+(x2-m,y2 )=(x1+x2-2m,y1+y2 ). +
+ )⊥
)⊥ ,可得 (
,可得 ( +
+ )•
)• =(x1+x2-2m,y1+y2 )•(x2-x1,y2-y1)
=(x1+x2-2m,y1+y2 )•(x2-x1,y2-y1) 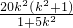 ,
,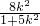 =-
=-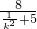 .∵k2>0,∴0<
.∵k2>0,∴0<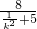 <
< ,
, <m<0. 故m的取值范围是[-
<m<0. 故m的取值范围是[- ,0).
,0).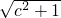 =
= ,求出c值,由离心率可得 a,求出b值,即得椭圆的标准方程.
,求出c值,由离心率可得 a,求出b值,即得椭圆的标准方程. +
+ )•
)• =0,解得 m=-
=0,解得 m=-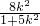 =-
=-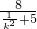 ,再利用不等式的性质求出m的取值范围.
,再利用不等式的性质求出m的取值范围.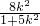 =-
=-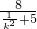 ,是解题的关键,
,是解题的关键,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 给出下列5个命题:
给出下列5个命题:![]() 的中心在坐标原点O,焦点在x轴上,离心率为
的中心在坐标原点O,焦点在x轴上,离心率为![]() ,P为椭圆上一动点,
,P为椭圆上一动点,![]() 、
、![]() 分别为椭圆的左、右焦点,且
分别为椭圆的左、右焦点,且![]() 面积的最大值为
面积的最大值为![]() .
. ![]() 的方程;
的方程;![]() 成等差数列,求动点M的轨迹
成等差数列,求动点M的轨迹![]() 的方程;
的方程;![]() 的切线
的切线![]() 交
交![]() 与Q、R两点,求证:
与Q、R两点,求证:![]() .
.