
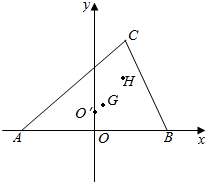
 如图,A,B,C的坐标分别为(-$\frac{c}{2}$,0),($\frac{c}{2}$,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心.
如图,A,B,C的坐标分别为(-$\frac{c}{2}$,0),($\frac{c}{2}$,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心.分析 (1)根据重心坐标公式即可求出,
(2)设外心O′,垂心H的坐标为(0,a),(m,b),根据向量的坐标运算得到$\overrightarrow{BC}$=(m-$\frac{c}{2}$,n),D的坐标为($\frac{c}{4}$+$\frac{m}{2}$,$\frac{n}{2}$),$\overrightarrow{O′D}$=($\frac{c}{4}$+$\frac{m}{2}$,$\frac{n}{2}$-a),$\overrightarrow{AH}$=(m+$\frac{c}{2}$,b),由题意得到由$\left\{\begin{array}{l}{\overrightarrow{O′D}•\overrightarrow{BC}=0}\\{\overrightarrow{AH}•\overrightarrow{BC}=0}\end{array}\right.$,化简计算得到即$\left\{\begin{array}{l}{a=\frac{4{m}^{2}+4{n}^{2}-{c}^{2}}{8n}}\\{b=\frac{-4{m}^{2}+{c}^{2}}{4n}}\end{array}\right.$,即可求出外心O′,垂心H的坐标;
(3)根据向量的坐标运算得到$\overrightarrow{GH}$=2$\overrightarrow{O′G}$,根据向量的共线条件即可证明.
解答 解:(1)重心G的坐标为($\frac{m}{3}$,$\frac{n}{3}$),
(2)设外心O′,垂心H的坐标为(0,a),(m,b),BC的中点为D,
∵A,B,C的坐标分别为(-$\frac{c}{2}$,0),($\frac{c}{2}$,0),(m,n),
∴$\overrightarrow{BC}$=(m-$\frac{c}{2}$,n),D的坐标为($\frac{c}{4}$+$\frac{m}{2}$,$\frac{n}{2}$),
∴$\overrightarrow{O′D}$=($\frac{c}{4}$+$\frac{m}{2}$,$\frac{n}{2}$-a),$\overrightarrow{AH}$=(m+$\frac{c}{2}$,b),
由$\left\{\begin{array}{l}{\overrightarrow{O′D}•\overrightarrow{BC}=0}\\{\overrightarrow{AH}•\overrightarrow{BC}=0}\end{array}\right.$,
则$\left\{\begin{array}{l}{(\frac{c}{4}+\frac{m}{2})(m-\frac{c}{2})+(\frac{n}{2}-a)•n=0}\\{(m+\frac{c}{2})(m-\frac{c}{2})+bn=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{a=\frac{4{m}^{2}+4{n}^{2}-{c}^{2}}{8n}}\\{b=\frac{-4{m}^{2}+{c}^{2}}{4n}}\end{array}\right.$,
∴外心O′的坐标为(0,$\frac{4{m}^{2}+4{n}^{2}-{c}^{2}}{8n}$),垂心H的坐标为(m,$\frac{-4{m}^{2}+{c}^{2}}{4n}$),
(3)由(1)(2)可知$\overrightarrow{GH}$=($\frac{2m}{3}$,$\frac{-12{m}^{2}-4{n}^{2}+3{c}^{2}}{12n}$),
$\overrightarrow{O′G}$=($\frac{m}{3}$,$\frac{-12{m}^{2}-4{n}^{2}+3{c}^{2}}{24m}$),
得$\overrightarrow{GH}$=2$\overrightarrow{O′G}$,
∴G,H,O′三点共线,且满足|GH|=2|OG′|.
点评 本题考查了向量在几何中的应用,关键是掌握坐标的运算法则和向量的数量积的运算,属于中档题.


 步步高达标卷系列答案
步步高达标卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{BC}$+$\overrightarrow{BA}$=$\overrightarrow{AC}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AD}$) | D. | $\overrightarrow{AD}$=$\overrightarrow{CB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
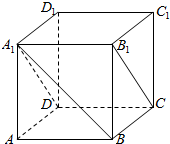 (1)在正方体ABCD-A1B1C1D1中,求直线A1B和平面A1B1CD所成的角的大小.(2)已知平面α,β,直线a,且α⊥β,α∩β=AB,a∥α,a⊥AB,试判断直线α与平面β的位置关系并证明.
(1)在正方体ABCD-A1B1C1D1中,求直线A1B和平面A1B1CD所成的角的大小.(2)已知平面α,β,直线a,且α⊥β,α∩β=AB,a∥α,a⊥AB,试判断直线α与平面β的位置关系并证明.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
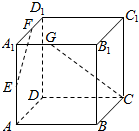 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AA1,A1D1,A1B1的中点,则异面直线EF与CG所成的角等于( )
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AA1,A1D1,A1B1的中点,则异面直线EF与CG所成的角等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边所成角为60°(如图所示),考虑到防洪堤的坚固性及石块用料等因素,设计其横断面要求面积为9$\sqrt{3}$m2,且髙度不低于$\sqrt{3}$m.问防洪堤横断面的腰长AB为多少时,横断面的外周长AB+BC+CD最小,并求最小外周长:
某地区要建造一条防洪堤,其横断面为等腰梯形,腰与底边所成角为60°(如图所示),考虑到防洪堤的坚固性及石块用料等因素,设计其横断面要求面积为9$\sqrt{3}$m2,且髙度不低于$\sqrt{3}$m.问防洪堤横断面的腰长AB为多少时,横断面的外周长AB+BC+CD最小,并求最小外周长:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com