
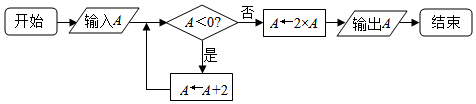
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
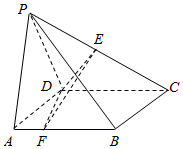 如图,在四棱锥P-ABCD中,底面ABCD是正方形,AD=PD=2,PA=2$\sqrt{2}$,∠PDC=120°,点E为线段PC的中点,点F在线段AB上.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,AD=PD=2,PA=2$\sqrt{2}$,∠PDC=120°,点E为线段PC的中点,点F在线段AB上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,$\sqrt{2}$) | C. | (0,2) | D. | (0,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{{k^2}+k+2}}{2}$ | B. | k2+k+2 | C. | $\frac{{{k^2}+k}}{6}$ | D. | $\frac{{{k^2}+1}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 某校高二1班55人,2班54人,3班52人,由此推出高二所有班级人数超过50人 | |
| B. | 在数列{an}中,a1=1,an+1=$\frac{a_n}{{1+{a_n}}}$(n=1,2,3,…),由此归纳数列{an}的通项公式 | |
| C. | 由平面三角形性质,推测空间四面体的性质 | |
| D. | 两直线平行,内错角相等,如果∠A与∠B是两条平行直线的内错角,则∠A=∠B |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com