
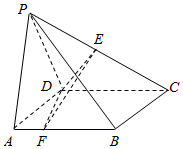
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,AD=PD=2,PA=2$\sqrt{2}$,∠PDC=120°,点E为线段PC的中点,点F在线段AB上.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,AD=PD=2,PA=2$\sqrt{2}$,∠PDC=120°,点E为线段PC的中点,点F在线段AB上.分析 (Ⅰ)过E作EH⊥CD于H,连结FH,推导出四边形AFHD是矩形,由此能证明CD⊥EF.
(Ⅱ)过D作DG⊥DC交PC于点G,以D为原点,以DA,DC,DG所在直线分别为x,y,z轴,建立空间直角坐标系O-xyz,利用向量法能求出当$AF=\frac{4}{3}$时,满足$cosθ=\frac{{\sqrt{3}}}{4}$.
解答 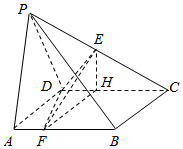 证明:(Ⅰ)在△PCD中,PD=CD=2,
证明:(Ⅰ)在△PCD中,PD=CD=2,
∵E为PC的中点,∴DE平分∠PDC,∠PDE=60°,
∴在Rt△PDE中,DE=PD•cos60°=1,…(2分)
过E作EH⊥CD于H,则$DH=\frac{1}{2}$,连结FH,
∵$AF=\frac{1}{2}$,∴四边形AFHD是矩形,…(4分)
∴CD⊥FH,又CD⊥EH,FH∩EH=H,∴CD⊥平面EFH,
又EF?平面EFH,∴CD⊥EF. …(5分)
解:(Ⅱ)∵AD=PD=2,$PA=2\sqrt{2}$,∴AD⊥PD,又AD⊥DC,
∴AD⊥平面PCD,
又AD?平面ABCD,∴平面PCD⊥平面ABCD. …(6分)
过D作DG⊥DC交PC于点G,则由平面PCD⊥平面ABCD知,DG⊥平面ABCD,
故DA,DC,DG两两垂直,以D为原点,以DA,DC,DG所在直线分别为x,y,z轴,
建立如图所示空间直角坐标系O-xyz,…(7分)
则A(2,0,0),B(2,2,0),C(0,2,0),$P(0,-1,\sqrt{3})$,
又知E为PC的中点,E$(0,\frac{1}{2},\frac{{\sqrt{3}}}{2})$,设F(2,t,0),
则$\overrightarrow{DE}=(0,\frac{1}{2},\frac{{\sqrt{3}}}{2})$,$\overrightarrow{DF}=(2,t,0)$,$h'(x)=\frac{1}{2}lnx$,$\overrightarrow{DA}=(2,0,0)$.…(8分)
设平面DEF的法向量为$\overrightarrow{n}$=(x1,y1,z1),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DE}=0}\\{\overrightarrow{n}•\overrightarrow{DF}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}\frac{1}{2}{y_1}+\frac{{\sqrt{3}}}{2}{z_1}=0\\ 2{x_1}+t{y_1}=0\end{array}\right.$,
取z1=-2,得平面DEF的一个法向量$n=(-\sqrt{3}t\;,\;2\sqrt{3}\;,\;-2)$,…(9分)
设平面ADP的法向量为$\overrightarrow{m}$=(x2,y2,z2),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{DP}=0}\\{\overrightarrow{m}•\overrightarrow{DA}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}-{y_2}+\sqrt{3}{z_2}=0\\ 2{x_2}=0\end{array}\right.$,
取z2=1,得$m=(0,\sqrt{3},1)$. …(10分)
∴$cosθ=|{cos<\overrightarrow m,\overrightarrow n>}|=\frac{{|{6-2}|}}{{2•\sqrt{3{t^2}+12+4}}}=\frac{{\sqrt{3}}}{4}$,解得$t=\frac{4}{3}$,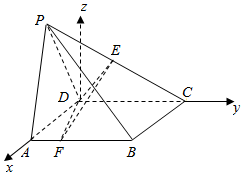
∴当$AF=\frac{4}{3}$时,满足$cosθ=\frac{{\sqrt{3}}}{4}$. …(12分)
点评 本题考查异面直线垂直的证明,考查满足角的余弦值的点是否存在的判断与求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
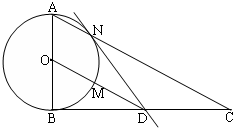 如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于N,过N作圆O的切线交BC于D,OD交圆O于点M.
如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于N,过N作圆O的切线交BC于D,OD交圆O于点M.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,-1]∪(2,3) | B. | [-2,-1)∪(2,3] | C. | (-2,-1]∪[2,3] | D. | (-2,-1)∪(2,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{1}{2}$ | B. | $\overrightarrow a⊥\overrightarrow b$ | C. | $\overrightarrow a∥\overrightarrow b$ | D. | $|{\overrightarrow a}|=|{\overrightarrow b}|$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com