
| A. | cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{1}{2}$ | B. | $\overrightarrow a⊥\overrightarrow b$ | C. | $\overrightarrow a∥\overrightarrow b$ | D. | $|{\overrightarrow a}|=|{\overrightarrow b}|$ |
分析 由已知求出cos<$\overrightarrow{a},\overrightarrow{b}$>,|$\overrightarrow{a}$|=$\sqrt{5}$,|$\overrightarrow{b}$|=$\sqrt{5}$,由此能求出结果.
解答 解:∵向量$\overrightarrow a$=(1,2,0),$\overrightarrow b$=(-2,0,1),
∴cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{-2}{\sqrt{5}•\sqrt{5}}$=-$\frac{2}{5}$,
故A、B、C都错误,
|$\overrightarrow{a}$|=$\sqrt{5}$,|$\overrightarrow{b}$|=$\sqrt{5}$,
∴|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=$\sqrt{5}$,故D正确.
故选:D.
点评 本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间向量的运算法则及性质的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
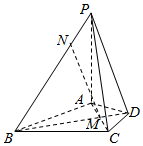 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=4,AB=4$\sqrt{3}$,∠CDA=120°,点N在线段PB上,且PN=2.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=4,AB=4$\sqrt{3}$,∠CDA=120°,点N在线段PB上,且PN=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
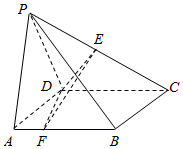 如图,在四棱锥P-ABCD中,底面ABCD是正方形,AD=PD=2,PA=2$\sqrt{2}$,∠PDC=120°,点E为线段PC的中点,点F在线段AB上.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,AD=PD=2,PA=2$\sqrt{2}$,∠PDC=120°,点E为线段PC的中点,点F在线段AB上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-4,\frac{17}{8}}]$ | B. | $(-∞,-4)∪(\frac{17}{8},+∞)$ | C. | [-4,4] | D. | (-∞,-4)∪(4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com