解:(1)f
1(x),f
2(x)是“三角形函数”,f
3(x)不是“三角形函数”.
任给三角形,设它的三边长分别为a,b,c,则a+b>c,不妨假设a≤c,b≤c,
由于
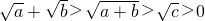
,所以f
1(x),f
2(x)是“保三角形函数”.
对于f
3(x),3,3,5可作为一个三角形的三边长,但3
2+3
2<5
2,
所以不存在三角形以3
2,3
2,5
2为三边长,故f
3(x)不是“保三角形函数”.
(2)设T>0为g(x)的一个周期,由于其值域为(0,+∞),
所以,存在n>m>0,使得g(m)=1,g(n)=2,
取正整数
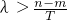
,可知λT+m,λT+m,n这三个数可作为一个三角形的三边长,
但g(λT+m)=1,g(λT+m)=1,g(n)=2不能作为任何一个三角形的三边长.
故g(x)不是“三角形函数”.
(3)当
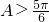
,
取
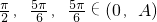
,显然这三个数可作为一个三角形的三边长,
但
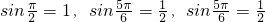
不能作为任何一个三角形的三边长,
故F(x)不是“三角形函数”.
分析:(1)任给三角形,设它的三边长分别为a,b,c,则a+b>c,不妨假设a≤c,b≤c,我们判断f(a),f(b),f(c)是否满足任意两数之和大于第三个数,即任意两边之和大于第三边;
(2)要想一个函数不是“三角形函数”关键是根据题中条件g(x)是定义在R上的周期函数,且值域为(0,+∞),举出反例;
(3)当
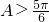
,取
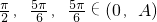
,显然这三个数可作为一个三角形的三边长,但
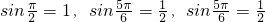
不能作为任何一个三角形的三边长,最后给出结论.
点评:本小题主要考查进行简单的合情推理、三角函数的性质等基础知识,考查运算求解能力,考查化归与转化思想.要想判断f(x)为“三角形函数”,要经过严密的论证说明f(x)满足“三角形函数”的概念,但要判断f(x)不为“三角形函数”,仅须要举出一个反例即可.

 ,f2(x)=x,f3(x)=x2中,哪些是“三角形函数”,哪些不是,并说明理由;
,f2(x)=x,f3(x)=x2中,哪些是“三角形函数”,哪些不是,并说明理由; 时,F(x)不是“三角形函数”.
时,F(x)不是“三角形函数”.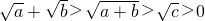 ,所以f1(x),f2(x)是“保三角形函数”.
,所以f1(x),f2(x)是“保三角形函数”.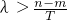 ,可知λT+m,λT+m,n这三个数可作为一个三角形的三边长,
,可知λT+m,λT+m,n这三个数可作为一个三角形的三边长,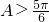 ,
,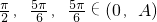 ,显然这三个数可作为一个三角形的三边长,
,显然这三个数可作为一个三角形的三边长,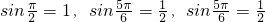 不能作为任何一个三角形的三边长,
不能作为任何一个三角形的三边长,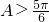 ,取
,取 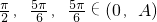 ,显然这三个数可作为一个三角形的三边长,但
,显然这三个数可作为一个三角形的三边长,但 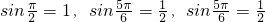 不能作为任何一个三角形的三边长,最后给出结论.
不能作为任何一个三角形的三边长,最后给出结论.

 ,f2(x)=x,f3(x)=x2中,哪些是“三角形函数”,哪些不是,并说明理由;
,f2(x)=x,f3(x)=x2中,哪些是“三角形函数”,哪些不是,并说明理由; 时,F(x)不是“三角形函数”.
时,F(x)不是“三角形函数”.