
【题目】设函数f(x)=x2﹣(m﹣1)x+2m
(1)若函数f(x)>0在(0,+∞)上恒成立,求m的取值范围;
(2)若函数f(x)在(0,1)内有零点,求m的取值范围.
【答案】
(1)解:∵函数f(x)>0在(0,+∞)上恒成立x2﹣(m﹣1)x+2m>0在(0,+∞)上恒成立,
m(x﹣2)<x2+x在(0,+∞)上恒成立,
①当x=2时,m∈R,
②x>2时,m< ![]() ,∵
,∵ ![]() ≥2
≥2 ![]() +5,∵m<2
+5,∵m<2 ![]() +5;
+5;
③0<x<2时,m> ![]() ,∵(x﹣2)+
,∵(x﹣2)+ ![]() =﹣[(2﹣x)+
=﹣[(2﹣x)+ ![]() ]<﹣5,
]<﹣5,
![]() <0,∴m≥0
<0,∴m≥0 ![]() +5
+5
综上可知,m的取值范围:0≤m<2 ![]() +5
+5
(2)解:函数f(x)在(0,1)内有零点,m(x﹣2)=x2+x在(0,1)上有解,m= ![]() 在(0,1)上有解.
在(0,1)上有解.
令2﹣x=t,t∈(1,2),函数g(t)=t+ ![]() ,t∈(1,2)时单调递减,g(t)=∈(5,7)
,t∈(1,2)时单调递减,g(t)=∈(5,7)
x∈(0,1), ![]() ∈(﹣2,0).
∈(﹣2,0).
故m的取值范围:(﹣2,0)
【解析】(1)函数f(x)>0在(0,+∞)上恒成立m(x﹣2)<x2+x在(0,+∞)上恒成立,按x=2,x>2时,0<x<2分类求解;(2)函数f(x)在(0,1)内有零点,m(x﹣2)=x2+x在(0,1)上有解,m= ![]() ,在(0,1)上有解.
,在(0,1)上有解.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)和y=g(x)在[﹣2,2]上的图象如图所示.给出下列四个命题: 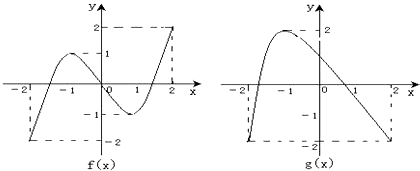
①方程f[g(x)]=0有且仅有6个根;
②方程g[f(x)]=0有且仅有3个根;
③方程f[f(x)]=0有且仅有5个根;
④方程g[g(x)]=0有且仅有4个根.
其中正确的命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若a,b,c∈R,f(a),f(b),f(c)为某一三角形的三边长,则称f(x)为“可构造三角形函数”,已知函数f(x)= ![]() 是“可构造三角形函数”,则实数t的取值范围是( )
是“可构造三角形函数”,则实数t的取值范围是( )
A.[0,+∞)
B.[0,1]
C.[1,2]
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点. 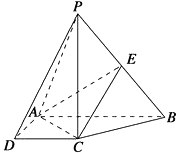
(1)求证:CE∥平面PAD;
(2)若二面角P﹣AC﹣E的余弦值为 ![]() ,求直线PA与平面EAC所成角的正弦值.
,求直线PA与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=kax﹣a﹣x(a>0且a≠1)是定义域为R的奇函数.
(1)若f(1)>0,试求不等式f(x2+2x)+f(x﹣4)>0的解集;
(2)若f(1)= ![]() ,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.
,且g(x)=a2x+a﹣2x﹣2mf(x)在[1,+∞)上的最小值为﹣2,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=f(x)图象上不同两点A(x1 , y1),B(x2 , y2)处的切线的斜率分别是kA , kB , 规定φ(A,B)= ![]() 叫曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: 1)函数y=x3﹣x2+1图象上两点A、B的横坐标分别为1,2,则φ(A,B)>
叫曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题: 1)函数y=x3﹣x2+1图象上两点A、B的横坐标分别为1,2,则φ(A,B)> ![]() ;
;
2)存在这样的函数,图象上任意两点之间的“弯曲度”为常数;
3)设点A、B是抛物线,y=x2+1上不同的两点,则φ(A,B)≤2;
4)设曲线y=ex上不同两点A(x1 , y1),B(x2 , y2),且x1﹣x2=1,若tφ(A,B)<1恒成立,则实数t的取值范围是(﹣∞,1);
以上正确命题的序号为(写出所有正确的)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com