设函数
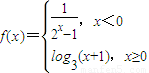
,则满足|f(x)|<2的x的取值范围是( )
A.(-∞,-1)∪[0,8)
B.(-∞,-1]∪[0,8]
C.(-∞,-1)(0,8)
D.(-∞,8)
【答案】
分析:由|f(x)|<2可得①
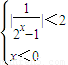
,或②
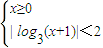
.分别求得①、②的解集,再取并集,即得所求.
解答:解:∵函数
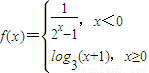
,则由|f(x)|<2可得①
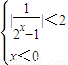
,或②
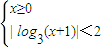
.
解①可得
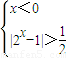
,解得 x<-1.
解②可得
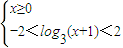
,解得 0≤x<8.
故原不等式的解集为 (-∞,-1)∪[0,8),
故选A.
点评:本题主要考查绝对值不等式的解法,体现了等价转化和分类讨论的数学而思想,属于中档题.
练习册系列答案
相关习题
科目:高中数学
来源:2011-2012学年吉林省吉林市普通中学高一(上)期末数学试卷(解析版)
题型:选择题
设函数

,则满足f(x)=

的x值为( )
A.
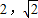
B.2
C.

D.±2
查看答案和解析>>
科目:高中数学
来源:2012-2013学年黑龙江省哈尔滨六中高三(上)期中数学试卷(理科)(解析版)
题型:选择题
设函数
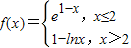
,则满足f(x)≤1的x的取值范围是( )
A.[1,2]
B.[0,2]
C.[1,+∞)
D.[0,+∞)
查看答案和解析>>
科目:高中数学
来源:2013-2014学年河南省郑州47中高三(上)第一次月考数学试卷(文科)(解析版)
题型:填空题
设函数
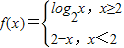
,则满足f(x)≤2的x的取值范围是
.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年黑龙江省哈尔滨六中高三(上)期中数学试卷(理科)(解析版)
题型:选择题
设函数
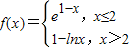
,则满足f(x)≤1的x的取值范围是( )
A.[1,2]
B.[0,2]
C.[1,+∞)
D.[0,+∞)
查看答案和解析>>
科目:高中数学
来源:2010年江苏省南通市如皋市高三1月抽考数学试卷(理科)(解析版)
题型:解答题
设函数
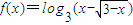
,则满足f(x)≥0的x的取值范围是
.
查看答案和解析>>

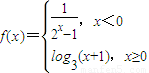 ,则满足|f(x)|<2的x的取值范围是( )
,则满足|f(x)|<2的x的取值范围是( ) 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案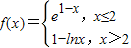 ,则满足f(x)≤1的x的取值范围是( )
,则满足f(x)≤1的x的取值范围是( )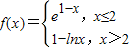 ,则满足f(x)≤1的x的取值范围是( )
,则满足f(x)≤1的x的取值范围是( )