
分析 由$\overrightarrow{AB}$•$\overrightarrow{AC}$=9,可得bccosA=9.又6=S△ABC=$\frac{1}{2}bc$sinA,可得tanA=$\frac{4}{3}$,bc=15.由sinB=cosA•sinC,利用正弦定理可得b=$\frac{3}{5}$c,联立解得b,c.利用余弦定理可得a.
由于$\overrightarrow{CP}$=x•$\frac{{\overrightarrow{CA}}}{{|\overrightarrow{CA}|}}$+y•$\frac{{\overrightarrow{CB}}}{{|\overrightarrow{CB}|}}$,可得$\overrightarrow{CP}$=$\frac{1}{3}x•\overrightarrow{CA}$+$\frac{1}{4}y$$\overrightarrow{CB}$,利用向量共线定理可得$\frac{1}{3}$x+$\frac{1}{4}$y=1.可得$\frac{3}{x}$+$\frac{4x}{3y}$=$\frac{3}{x}+\frac{4x}{12-4x}$=$\frac{3}{x}+\frac{x}{3-x}$=f(x),利用导数研究函数的单调性即可得出.
解答 解:∵$\overrightarrow{AB}$•$\overrightarrow{AC}$=9,∴bccosA=9,
∵6=S△ABC=$\frac{1}{2}bc$sinA,
∴tanA=$\frac{4}{3}$,
∴sinA=$\frac{4}{5}$,cosA=$\frac{3}{5}$.
∴bc=15.
∵sinB=cosA•sinC,
∴b=$\frac{3}{5}$c,
$\left\{\begin{array}{l}{bc=15}\\{b=\frac{3}{5}c}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=3}\\{c=5}\end{array}\right.$.
∴a2=b2+c2-2bccosA=32+52-18=16.
∴a=4.
∵$\overrightarrow{CP}$=x•$\frac{{\overrightarrow{CA}}}{{|\overrightarrow{CA}|}}$+y•$\frac{{\overrightarrow{CB}}}{{|\overrightarrow{CB}|}}$,
∴$\overrightarrow{CP}$=$\frac{1}{3}x•\overrightarrow{CA}$+$\frac{1}{4}y$$\overrightarrow{CB}$,
∴$\frac{1}{3}$x+$\frac{1}{4}$y=1.
∴3y=12-4x>0.解得0<x<3.
则$\frac{3}{x}$+$\frac{4x}{3y}$=$\frac{3}{x}+\frac{4x}{12-4x}$=$\frac{3}{x}+\frac{x}{3-x}$=f(x),
f′(x)=-$\frac{3}{{x}^{2}}$+$\frac{3}{(3-x)^{2}}$=$\frac{9(2x-3)}{(3x-{x}^{2})^{2}}$,
当$\frac{3}{2}<x<3$时,f′(x)>0,函数f(x)单调递增;当$0<x<\frac{3}{2}$时,f′(x)<0,函数f(x)单调递减.
∴当x=$\frac{3}{2}$时,f(x)取得最小值,$f(\frac{3}{2})$=3.
故答案为:3.
点评 本题考查了向量数量积运算性质、正弦定理、余弦定理、向量共线定理、利用导数研究函数的单调性,考查了推理能力与计算能力,属于难题.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
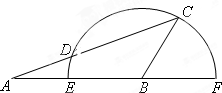 如图,在△ABC中,AB=5,BC=3,∠ABC=120°,以点B为圆心,线段BC的长为半径的半圆交AB所在直线于点E、F,交线段AC于点D,则线段AD的长为$\frac{16}{7}$.
如图,在△ABC中,AB=5,BC=3,∠ABC=120°,以点B为圆心,线段BC的长为半径的半圆交AB所在直线于点E、F,交线段AC于点D,则线段AD的长为$\frac{16}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com