练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设点O在△ABC的内部且有4
    OA
    +
    OB
    +
    OC
    =0    ，则的△ABC面积与△OBC的面积之比是
    3：1
    3：1
    ．
    分析：取BC中点为D，则
    OB
    +
    OC
    =2
    OD
    ，利用4
    OA
    +
    OB
    +
    OC
    =0    ，可得△ABC的高与△OBC的高之比，从而可得△ABC的面积与△OBC的面积之比．
    解答：解：取BC中点为D，则
    OB
    +
    OC
    =2
    OD

    ∵4
    OA
    +
    OB
    +
    OC
    =0
    ∴4
    OA
    +2
    OD
    =0
    ∴
    OD
    =-2
    OA

    ∴△ABC的高与△OBC的高之比为3：2
    ∴△ABC的面积与△OBC的面积之比为3：2
    故答案为：3：2
    点评：本题考查向量知识的运用，考查三角形面积的计算，解题的关键是利用向量的加法法则，确定三点共线．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网在平面向量中有如下定理：设点O、P、Q、R为同一平面内的点，则P、Q、R三点共线的充要条件是：存在实数t，使
    OP
    =(1-t)
    OQ
    +t
    OR
    ．试利用该定理解答下列问题：
    如图，在△ABC中，点E为AB边的中点，点F在AC边上，且CF=2FA，BF交CE于点M，设
    AM
    =x
    AE
    +y
    AF
    ，则x+2y=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

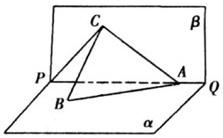    精英家教网如图所示，PQ为平面α、β的交线，已知二面角α-PQ-β为直二面角，A∈PQ，B∈α，C∈β，CA=CB=kAB（k∈R*），∠BAP=45°．
    （1）证明：BC⊥PQ；
    （2）设点C在平面α内的射影为点O，当k取何值时，O在平面ABC内的射影G恰好为△ABC的重心？
    （3）当k=
    		6
    3
    时，求二面角B-AC-P的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•惠州二模）在平面向量中有如下定理：设点O，P，Q，R为同一平面内的点，则P，Q，R三点共线的充要条件是：存在实数t，使
    OP
    =(1-t)
    OQ
    +t
    OR
    ．如图，在△ABC中，点E为AB边的中点，点F在AC边上，且CF=2FA，BF交CE于点M，设
    AM
    =x
    AE
    +y
    AF
    ，则（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

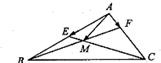
    在平面向量中有如下定理：设点O，P，Q，R为同一平面内的点，则P、Q、R三点共线的充要条件是：存在实数t，使.试利用该定理解答下列问题：如图，

     


    在ΔABC中，点E为AB边的中点，点F在AC边上，且CF＝2FA，BF交CE于点M，设，则x＋y＝     .

    查看答案和解析>>

    科目：高中数学 来源：2010年湖北省高一下学期期末考试数学试卷 题型：解答题

    (本小题13分) 如图所示, PQ为平面的交线, 已知二面角为直二面角,  , ∠BAP＝45°.

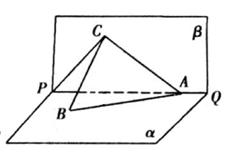
    （1）证明: BC⊥PQ;

    （2）设点C在平面内的射影为点O, 当k取何值时, O在平面ABC内的射影G恰好为△ABC的重心？

    （3）当时, 求二面角B－AC－P的大小.

     

    查看答案和解析>>

    同步练习册答案