
 =(1,7),
=(1,7), =(5,1),
=(5,1), =(2,1),点X为直线OP上的一个动点.
=(2,1),点X为直线OP上的一个动点. •
•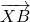 取最小值时,求
取最小值时,求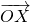 的坐标;
的坐标;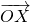 =(x,y),
=(x,y),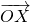 与
与  共线.
共线. =(2,1),∴x-2y=0,即x=2y.
=(2,1),∴x-2y=0,即x=2y.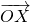 =(2y,y).又
=(2y,y).又  =
= -
-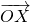 ,
, =(1,7),
=(1,7), =(1-2y,7-y).
=(1-2y,7-y).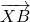 =
= -
-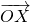 =(5-2y,1-y).
=(5-2y,1-y). •
•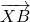 =(1-2y)(5-2y)+(7-y)(1-y)=5y2-20y+12=5(y-2)2-8.
=(1-2y)(5-2y)+(7-y)(1-y)=5y2-20y+12=5(y-2)2-8. •
•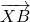 有最小值-8,此时
有最小值-8,此时 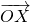 =(4,2).
=(4,2).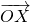 =(4,2),即y=2时,有
=(4,2),即y=2时,有  =(-3,5),
=(-3,5),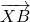 =(1,-1).
=(1,-1). |=
|= ,|
,|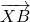 |=
|= .
.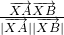 =-
=-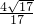 .
.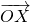 与
与  共线,可以得到关于
共线,可以得到关于 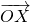 坐标的一个关系式,再根据
坐标的一个关系式,再根据  •
•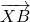 的最小值,求得
的最小值,求得 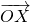 的坐标,
的坐标, 与
与 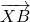 夹角的余弦,利用数量积的知识易解决.
夹角的余弦,利用数量积的知识易解决. 与
与 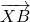 反向时,
反向时, •
•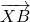 有最小值进行求解.而(2)中即为数量积定义的应用.
有最小值进行求解.而(2)中即为数量积定义的应用. 

 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
| OA |
| OB |
| OP |
| XA |
| XB |
| OX |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)当![]() ·
·![]() 取最小时,求
取最小时,求![]() 的坐标;
的坐标;
(2)当点X满足(1)的条件和结论时,求∠AXB的余弦值.
查看答案和解析>>
科目:高中数学 来源:2013届山东省高一下学期期末考试数学 题型:解答题
平面内有向量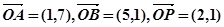 ,点M为直线OP上的一个动点.
,点M为直线OP上的一个动点.
(1)当 取得最小值时,求点M的坐标;
取得最小值时,求点M的坐标;
(2)在点M满足(1)的条件下,求 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| OA |
| OB |
| OP |
| XA |
| XB |
| OX |
查看答案和解析>>
科目:高中数学 来源:2011届江西省安福中学高三第三次月考联考文科数学卷 题型:解答题
(本大题满分12分)
平面内有向量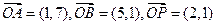 ,点X为直线OP上的一动点。
,点X为直线OP上的一动点。
(1)当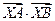 取最小值时,求
取最小值时,求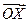 的坐标;
的坐标;
(2)当点X满足(1)的条件和结论时,求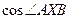 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com