【错解分析】错解一:原不等式可化为
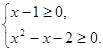
, 解得x≥2.
∴原不等式的解集是{x|x≥2}.
此解中,当x =" -" 1时,原不等式也成立,漏掉了x =" -" 1这个解.原因是忽略了不等式中“≥”具有相等与不相等的双重性.事实上,
不等式f(x)·
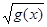
≥0与

或g(x) = 0同解.
错解二:在不等式f(x)·
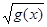
≥0中,按f(x)的取值情况分类,
有
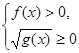
,或

.
当x – 1 > 0,即x > 1时,原不等式等价于x
2 – x – 2 ≥ 0,解得x ≥ 2;
当x – 1 = 0,即x = 1时,显然
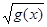
无意义,其解集为
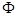
.
综上所述,原不等式的解集为{x|x ≥ 2}.
此解中分类不全,有遗漏,应补充第三种情况
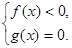
即当x – l < 0,且x
2 – x – 2 = 0时也合乎条件,即补上x =" -" 1.
故原不等式的解集为{x|x≥2,或x =" -" 1}.
【正解】分析一:符号“≥”是由符号“>”“ = ”合成的,故不等式f(x)·
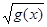
≥ 0可转化为f(x)·
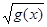
> 0或f(x)·
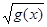
= 0.
正解一:原不等式可化为(I)(x-1)
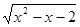
> 0,或(Ⅱ)(x - 1)
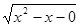
= O.
(I)中,由
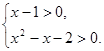
得x > 2; (Ⅱ)中,由x
2 – x – 2 = 0,或x – 1 = O,
且x
2 – x - 2有意义,得x = 1,或x = 2.
∴原不等式的解集为{x|x≥2,或x =" -" 1}.
分析二:在不等式f(x)·
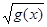
≥0中,按g(x)的取值情况分类,有两种情况:
(1)g(x) > 0时,等式等价于
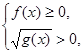
(2)g(x) = 0时'只须f(x)有意义即可.
正解二:分两种情况讨论.
(1)当x
2 – x – 2 > 0,即x > 2,或x < - 1时,原不等式等价于
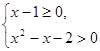
.
解得x > 2.
(2)当x
2 – x – 2 = 0,即x = 2,或x =" -" 1时,显然有意义,是原不等式的解.
综上所述.原不等式的解集是{x|x≥2,或x =" -" 1}.
【点评】在解不等式的过程中,要充分运用自己的分析能力,把原不等式等价地转化为易解的不等式,这中间一定是等价转化,否则如果对某个知识点遗漏掉,便极易出错。

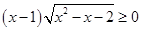 .
.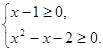 , 解得x≥2.
, 解得x≥2.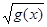 ≥0与
≥0与 或g(x) = 0同解.
或g(x) = 0同解.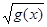 ≥0中,按f(x)的取值情况分类,
≥0中,按f(x)的取值情况分类,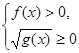 ,或
,或 .
.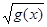 无意义,其解集为
无意义,其解集为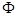 .
.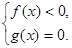
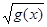 ≥ 0可转化为f(x)·
≥ 0可转化为f(x)·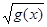 > 0或f(x)·
> 0或f(x)·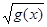 = 0.
= 0.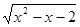 > 0,或(Ⅱ)(x - 1)
> 0,或(Ⅱ)(x - 1)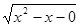 = O.
= O.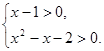 得x > 2; (Ⅱ)中,由x2 – x – 2 = 0,或x – 1 = O,
得x > 2; (Ⅱ)中,由x2 – x – 2 = 0,或x – 1 = O,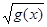 ≥0中,按g(x)的取值情况分类,有两种情况:
≥0中,按g(x)的取值情况分类,有两种情况: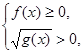 (2)g(x) = 0时'只须f(x)有意义即可.
(2)g(x) = 0时'只须f(x)有意义即可.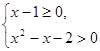 .
.
