Question

在半径为R的圆内接正六边形内，依次连接各边的中点，得一正六边形，又在这一正六边形内，再依次连接各边的中点，又得一正六边形，这样无限地继续下去，求：
（1）前n个正六边形的周长之和S_n；
（2）所有这些正六边形的周长之和S．

Answer 1

分析：由题设条件知表示正六边形周长的数列：6R，6R•

3

2

，6R•(

3

2

)2，6R•(

3

2

)3，6R•(

3

2

)n-1，由此能够求出前n个正六边形周长的和与所有这些正六边形周长的和．

解答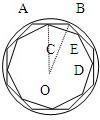：解：如图，半径为R的圆内接正六边形的周长为6R，
设C为AB的中点，连接OC，OB，则OC⊥AB．
∴OC=CD=R•sin60°=

3

2

R．
第二个正六边形的周长=6R•

3

2

．
同理可得
第三个正六边形的周长=6R•(

3

2

)2，
第四个正六边形的周长=6R•(

3

2

)3，
于是可以得到一个表示正六边形周长的数列：
6R，6R•

3

2

，6R•(

3

2

)2，6R•(

3

2

)3，6R•(

3

2

)n-1，
①前n个正六边形周长的和Sn=6R+6R•

3

2

+6R•(

3

2

)2+…+6R•(

3

2

)n-1=6R[1+

3

2

+(

3

2

)2+…+(

3

2

)n-1]=6R•

1-( 3 2 )n

1- 3 2

=12(2+

3

)[1-(

3

2

)n]R．
②所有这些正六边形周长的和S=

6R

1- 3 2

=

12R

2- 3

=12(2+

3

)R．

点评：本题考查数列的性质和运用，解题时要注意归纳、总结能力的培养．