
【题目】在四棱锥![]() 中,四边形
中,四边形![]() 为菱形,且
为菱形,且![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() ,
,![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,
,![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
【答案】(1)见证明(2)![]()
【解析】
(1)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() ,先证明
,先证明![]() ,即证
,即证![]() 平面
平面![]() ;(2)连接
;(2)连接![]() ,
,![]() ,设
,设![]() ,连接
,连接![]() ,连接
,连接![]() . 分别以
. 分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的非负半轴,建立如图所示的空间直角坐标系
轴的非负半轴,建立如图所示的空间直角坐标系![]() .再利用向量方法求平面
.再利用向量方法求平面![]() 与平面
与平面![]() 所成二面角的正弦值为
所成二面角的正弦值为![]() .
.
(1)证明:设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() .
.
∵![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴![]() ,且
,且![]() .
.
由已知得![]() ,且
,且![]() .
.
∴![]() ,且
,且![]() .
.
∴四边形![]() 是平行四边形.
是平行四边形.
∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
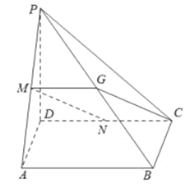
(2)连接![]() ,
,![]() ,设
,设![]() ,连接
,连接![]() ,连接
,连接![]() .
.
设菱形![]() 的边长为
的边长为![]() ,由题设得
,由题设得![]() ,
,![]() ,
,![]() ,
,
![]() 平面
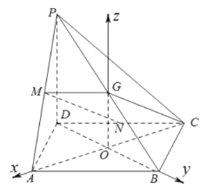
平面![]() ,分别以
,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的非负半轴,建立如图所示的空间直角坐标系
轴的非负半轴,建立如图所示的空间直角坐标系![]() .
.
由题设得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
设![]() 是平面
是平面![]() 的法向量,
的法向量,
则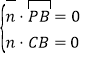 ,化简得
,化简得![]() ,
,
令![]() ,则
,则![]() ,
,![]() .∴
.∴![]() .
.
同理可求得平面![]() 的一个法向量
的一个法向量![]() .
.
∴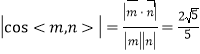 .
.
∴平面![]() 与平面
与平面![]() 所成二面角的正弦值为
所成二面角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】2019年春节期间,我国高速公路继续执行“节假日高速免费政策”.某路桥公司为掌握春节期间车辆出行的高峰情况,在某高速收费点处记录了大年初三上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如图所示,其中时间段9:20~9:40记作区间![]() ,9:40~10:00记作
,9:40~10:00记作![]() ,10:00~10:20记作
,10:00~10:20记作![]() ,10:20~10:40记作
,10:20~10:40记作![]() .比方:10点04分,记作时刻64.
.比方:10点04分,记作时刻64.
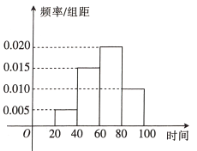
(1)估计这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值(同一组中的数据用该组区间的中点值代表);
(2)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车中随机抽取4辆,记![]() 为9:20~10:00之间通过的车辆数,求
为9:20~10:00之间通过的车辆数,求![]() 的分布列与数学期望;
的分布列与数学期望;
(3)由大数据分析可知,车辆在春节期间每天通过该收费点的时刻![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,
可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,![]() 可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左焦点为
的左焦点为![]() ,过点F做x轴的垂线交椭圆于A,B两点,且
,过点F做x轴的垂线交椭圆于A,B两点,且![]() .
.
(1)求椭圆C的标准方程:
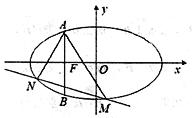
(2)若M,N为椭圆上异于点A的两点,且直线![]() 的倾斜角互补,问直线MN的斜率是否为定值?若是,求出这个定值;若不是,请说明理由.
的倾斜角互补,问直线MN的斜率是否为定值?若是,求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某轮船公司年初以200万元购进一艘轮船,以每年40万元的价格出租给海运公司.轮船公司负责轮船的维护,第一年维护费为4万元,随着轮船的使用与磨损,以后每年的维护费比上一年多2万元,同时该轮船第![]() 年末可以以
年末可以以![]() 万元的价格出售.
万元的价格出售.
(1)写出轮船公司到第![]() 年末所得总利润
年末所得总利润![]() 万元关于
万元关于![]() 的函数解析式,并求
的函数解析式,并求![]() 的最大值;
的最大值;
(2)为使轮船公司年平均利润最大,轮船公司应在第几年末出售轮船?
查看答案和解析>>
科目:高中数学 来源: 题型:
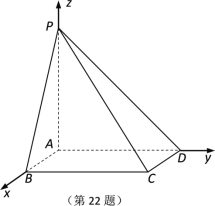
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,AB 1,AP AD 2.
,AB 1,AP AD 2.
(1)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若点M,N分别在AB,PC上,且![]() 平面
平面![]() ,试确定点M,N的位置.
,试确定点M,N的位置.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面立角坐标系![]() 中,过点
中,过点![]() 的圆的圆心
的圆的圆心![]() 在
在![]() 轴上,且与过原点倾斜角为
轴上,且与过原点倾斜角为![]() 的直线
的直线![]() 相切.
相切.
(1)求圆![]() 的标准方程;
的标准方程;
(2)点![]() 在直线
在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线
的切线![]() 、
、![]() ,切点分别为
,切点分别为![]() 、
、![]() ,求经过
,求经过![]() 、
、![]() 、
、![]() 、
、![]() 四点的圆所过的定点的坐标.
四点的圆所过的定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定数列![]() ,若满足
,若满足![]() 且
且![]() ,对于任意的n,
,对于任意的n,![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为“指数型数列”.
为“指数型数列”.
![]() Ⅰ
Ⅰ![]() 已知数列
已知数列![]() ,
,![]() 的通项公式分别为
的通项公式分别为![]() ,
,![]() ,试判断
,试判断![]() ,
,![]() 是不是“指数型数列”;
是不是“指数型数列”;
![]() Ⅱ
Ⅱ![]() 若数列
若数列![]() 满足:
满足:![]() ,
,![]() ,判断数列
,判断数列![]() 是否为“指数型数列”,若是给出证明,若不是说明理由;
是否为“指数型数列”,若是给出证明,若不是说明理由;
![]() Ⅲ
Ⅲ![]() 若数列
若数列![]() 是“指数型数列”,且
是“指数型数列”,且![]() ,证明:数列
,证明:数列![]() 中任意三项都不能构成等差数列.
中任意三项都不能构成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“工资条里显红利,个税新政人民心”.随着2019年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段.2019年1月1日实施的个税新政主要内容包括:(1)个税起征点为5000元;(2)每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除;(3)专项附加扣除包括住房、子女教育和赡养老人等.
新旧个税政策下每月应纳税所得额(含税)计算方法及其对应的税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
缴税级数 | 每月应纳税所得额(含税)=收入-个税起征点 | 税率(%) | 每月应纳税所得额(含税)=收入-个税起征点-专项附加扣除 | 税率(%) |
1 | 不超过1500元部分 | 3 | 不超过3000元部分 | 3 |
2 | 超过1500元至4500元部分 | 10 | 超过3000元至12000元部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元至55000元部分 | 30 | 超过35000元至55000元部分 | 30 |
··· | ··· | ··· | ··· | ··· |
随机抽取某市1000名同一收入层级的![]() 从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等。
从业者的相关资料,经统计分析,预估他们2019年的人均月收入24000元.统计资料还表明,他们均符合住房专项扣除;同时,他们每人至多只有一个符合子女教育扣除的孩子,并且他们之中既不符合子女教育扣除又不符合赡养老人扣除、只符合子女教育扣除但不符合赡养老人扣除、只符合赡养老人扣除但不符合子女教育扣除、即符合子女教育扣除又符合赡养老人扣除的人数之比是2:1:1:1;此外,他们均不符合其他专项附加扣除.新个税政策下该市的专项附加扣除标准为:住房1000元/月,子女教育每孩1000元/月,赡养老人2000元/月等。
假设该市该收入层级的![]() 从业者都独自享受专项附加扣除,将预估的该市该收入层级的
从业者都独自享受专项附加扣除,将预估的该市该收入层级的![]() 从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
从业者的人均月收入视为其个人月收入.根据样本估计总体的思想,解决如下问题:
(1)设该市该收入层级的![]() 从业者2019年月缴个税为
从业者2019年月缴个税为![]() 元,求
元,求![]() 的分布列和期望;
的分布列和期望;
(2)根据新旧个税方案,估计从2019年1月开始,经过多少个月,该市该收入层级的![]() 从业者各月少缴交的个税之和就超过2019年的月收入?
从业者各月少缴交的个税之和就超过2019年的月收入?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com