
己知L1、L2是过点P(-![]() ,0)的两条互相垂直的直线,且L1、L2与双曲线y2-x2=1各有两个交点,且分别为A1、B1和A2、B2。
,0)的两条互相垂直的直线,且L1、L2与双曲线y2-x2=1各有两个交点,且分别为A1、B1和A2、B2。
(1)求L1的斜率k1的取值范围;
(2)若A1恰是双曲线的一个顶点,求|A2B2|的值。
解:(1)据题意,L1、L2的斜率都存在, 因为L1过点P(-
有两个不同的解。 在方程组①中,消去y,整理得 (k12-1)x2+2 若k12-1=0,直线与双曲线的渐近线平行,与双曲线只有一个交点,与题设矛盾。故k12-1≠0,即|k1|≠1 方程②的判别式为 △1=(2 =4(3k12-1) 设L2的斜率为k2,因为L2过点P(-
有两个不同的解。 在方程组③中消去y,整理得 (k22-1)x2+2 同理有k22-1≠0,△2=4(3k22-1) 因为L1⊥L2,所以有k1·k2=-1,于是L1、L2与双曲线各有两个交点的充要条件是
∴k1∈(- (2)双曲线y2-x2=1的顶点为(0,-1)、(0,1),取A1(0,1)时,有k1(0+ 解得k1= ∴k2=- x2+4 设L2与双曲线的两个交点的坐标为A2(x1,y1)、B2(x2,y2), 则x1+x2=-4 ∴|A2B2|= =3 当取A1(0,-1)时,由双曲线y2-x2=1关于x轴对称,知|A2B2|=2 ∴L1过双曲线的一个顶点时,|A2B2|=2 |


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
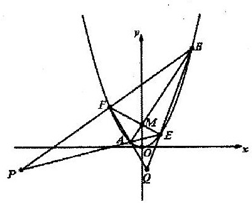 (2012•浙江模拟)己知抛物线C:x2=2py(p>0)上一点T(m,4)到其焦点的距离为
(2012•浙江模拟)己知抛物线C:x2=2py(p>0)上一点T(m,4)到其焦点的距离为| 17 |
| 4 |
| MP |
| MQ |
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
(1)求L1的斜率k1的取值范围;
(2)若A1恰是双曲线的一个顶点,求|A2B2|的值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
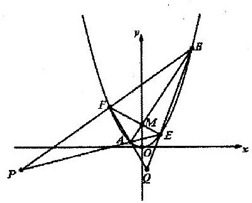 己知抛物线C:x2=2py(p>0)上一点T(m,4)到其焦点的距离为
己知抛物线C:x2=2py(p>0)上一点T(m,4)到其焦点的距离为 .
.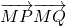 是定值.
是定值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省稽阳联谊学校高三联考数学试卷(文科)(解析版) 题型:解答题
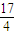 .
. 是定值.
是定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com