练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．72015+${C}_{2015}^{1}$72014+${C}_{2013}^{2}$72013+…+${C}_{2015}^{2014}$•7除以9得余数是7．

    分析 所给的式子即（9-1）2015-1，按照二项式定理展开，可得它除以9的余数．

    解答 解：72015+${C}_{2015}^{1}$72014+${C}_{2013}^{2}$72013+…+${C}_{2015}^{2014}$•7=（7+1）2015-1=（9-1）2015-1
    =${C}_{2015}^{0}$•92015-${C}_{2015}^{1}$•92014+${C}_{2015}^{2}$•92013+…+（-1）n•${C}_{2015}^{n}$•92015-n+…+${C}_{2015}^{2014}$•9-2，
     除了最后一项外，其余的各项都能被9整除，故它除以9的余数为7，
    故答案为：7．

    点评 本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．设关于x的二次方程px2+（p-1）x+p+1=0有两个不相等的正根，且一根大于另一根的两倍，求p的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

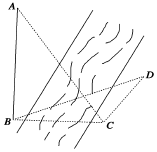    14．如图，为测得河对岸塔AB的高，先在河岸上选一点，C使在塔底的正东方向上，测得点的仰角为60°，再由点沿北偏东15°方向走10米到位置，测得∠BDC=45°，若AB⊥平面BCD，则塔AB的高是$10\sqrt{6}$米．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．函数y=x2+2x-4，x∈[-2，2]的值域为（　　）
    A．[-5，4]B．[-4，4]C．[-4，+∞）D．（-∞，4]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．在同一坐标系内，函数y=xa（a＜0）和y=ax-1的图象可能是下图中的（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．设圆C与两圆（x+$\sqrt{5}$）2+y2=4，（x-$\sqrt{5}$）2+y2=4中的一个内切，另一个外切，求圆心C的轨迹L的方程．

    查看答案和解析>>

    科目：高中数学 来源：2017届山东临沭一中高三上学期10月月考数学（文）试卷（解析版） 题型：选择题

    向量，，若，则（ )

    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源：2017届江西吉安一中高三上学期段考一数学（文）试卷（解析版） 题型：填空题

    已知函数（其中为自然对数的底数），则函数的零点等于____________．

    查看答案和解析>>

    科目：高中数学 来源：2017届江苏南通市如东县等高三10月联考数学试卷（解析版） 题型：解答题

    已知函数．

    （1） 求函数的单调递减区间；

    （2） 当时，的最小值是，求实数的值．

    查看答案和解析>>

    同步练习册答案