
分析 根据两圆的方程分别找出两圆心和两半径,根据两圆内切时,两圆心之间的距离等于两半径相减,外切时,两圆心之间的距离等于两半径相加,可知圆心C到圆心F1的距离加2与圆心C到圆心F2的距离减2或圆心C到圆心F1的距离减2与圆心C到圆心F2的距离加2,得到圆心C到两圆心的距离之差为常数4,且小于两圆心的距离2$\sqrt{5}$,可知圆心C的轨迹为以原点为中心,焦点在x轴上的双曲线,根据a与c的值求出b的值,写出轨迹L的方程即可.
解答 解:(1)两圆的半径都为2,两圆心为F1(-$\sqrt{5}$,0)、F2($\sqrt{5}$,0),
由题意得:|CF1|+2=|CF2|-2或|CF2|+2=|CF1|-2,
∴||CF2|-|CF1||=4=2a<|F1F2|=2$\sqrt{5}$=2c,
可知圆心C的轨迹是以原点为中心,焦点在x轴上,且实轴为4,焦距为2$\sqrt{5}$的双曲线,
因此a=2,c=$\sqrt{5}$,则b2=c2-a2=1,
所以轨迹L的方程为$\frac{{x}^{2}}{4}$-y2=1.
点评 此题考查学生会根据已知条件得到动点的轨迹方程,掌握双曲线的简单性质,灵活运用两点间的距离公式及三角形的两边之和大于第三边,两边之差小于第三边解决实际问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届山东临沭一中高三上学期10月月考数学(文)试卷(解析版) 题型:选择题
已知函数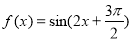 (
(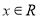 ),下面结论错误的是( )
),下面结论错误的是( )
A.函数 的最小正周期为
的最小正周期为
B.函数 是偶函数
是偶函数
C.函数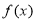 的图象关于直线
的图象关于直线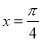 对称
对称
D.函数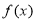 在区间
在区间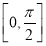 上是增函数
上是增函数
查看答案和解析>>
科目:高中数学 来源:2017届山东临沭一中高三上学期10月月考数学(文)试卷(解析版) 题型:选择题
在等差数列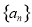 中,已知
中,已知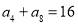 ,则该数列前
,则该数列前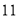 项和
项和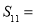 ( )
( )
A.58 B.88 C.143 D.176
查看答案和解析>>
科目:高中数学 来源:2017届江西吉安一中高三上学期段考一数学(文)试卷(解析版) 题型:选择题
已知椭圆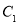 与双曲线
与双曲线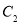 有相同的焦点
有相同的焦点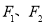 ,点
,点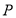 是
是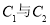 的一个公共点,
的一个公共点,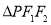 是以一个以
是以一个以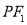 为底的等腰三角形,
为底的等腰三角形,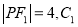 的离心率为
的离心率为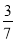 ,则
,则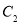 的离心率是( )
的离心率是( )
A.2 B.3 C. D.
D.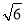
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com