练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．已知在复平面内i是虚数单位，复数z=$\frac{1+ai}{1-i}$（a∈R）对应的点在直线x-y=1，则a=（　　）
    A．-2B．-1C．1D．2

    分析 利用复数代数形式的乘除运算化简复数z，求出对应的点的坐标，再由对应的点在直线x-y=1，列出方程求解即可得答案．

    解答 解：复数z=$\frac{1+ai}{1-i}$=$\frac{（1+ai）（1+i）}{（1-i）（1+i）}$=$\frac{（1-a）+（a+1）i}{2}$=$\frac{1-a}{2}+\frac{a+1}{2}i$，
    对应的点（$\frac{1-a}{2}$，$\frac{a+1}{2}$）在直线x-y=1上，
    ∴$\frac{1-a}{2}$-$\frac{a+1}{2}$=1，
    解得a=-1．
    故选：B．

    点评 本题考查了复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    11．已知直线l过点P（3，6）且与x，y轴的正半轴分别交于A、B两点，O是坐标原点，则当|OA|+|OB|取得最小值时的直线方程是$\sqrt{2}$x+y-6-3$\sqrt{2}$=0（用一般式表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知集合A={x|x2-3x-10≤0}，B={x|m-4≤x≤3m+2}．
    （1）若A∪B=B，求实数m的取值范围；
    （2）若A∩B=B，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．函数f（x）=$\frac{2x+1}{\sqrt{（lo{g}_{3}x）^{2}-4}}$的定义域为（　　）
    A．（$\frac{1}{9}$，9）B．[$\frac{1}{9}$，9]C．（0，$\frac{1}{9}$]∪[9，+∞）D．（0，$\frac{1}{9}$）∪（9，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

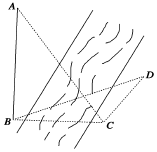    14．如图，为测得河对岸塔AB的高，先在河岸上选一点，C使在塔底的正东方向上，测得点的仰角为60°，再由点沿北偏东15°方向走10米到位置，测得∠BDC=45°，若AB⊥平面BCD，则塔AB的高是$10\sqrt{6}$米．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的表面积为96+4（$\sqrt{2}$-1）π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．函数y=x2+2x-4，x∈[-2，2]的值域为（　　）
    A．[-5，4]B．[-4，4]C．[-4，+∞）D．（-∞，4]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．设圆C与两圆（x+$\sqrt{5}$）2+y2=4，（x-$\sqrt{5}$）2+y2=4中的一个内切，另一个外切，求圆心C的轨迹L的方程．

    查看答案和解析>>

    科目：高中数学 来源：2017届江西吉安一中高三上学期段考一数学（理）试卷（解析版） 题型：解答题

    设函数，已知在处的切线相同．

    （1）求的值及切线的方程；

    （2）设函数，若存在实数使得关于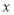的不等式对上的任意实数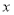恒成立，求的最小值及对应的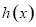的解析式．

    查看答案和解析>>

    同步练习册答案